Tính chất đường cao trong tam giác cân

Mô tả sản phẩm

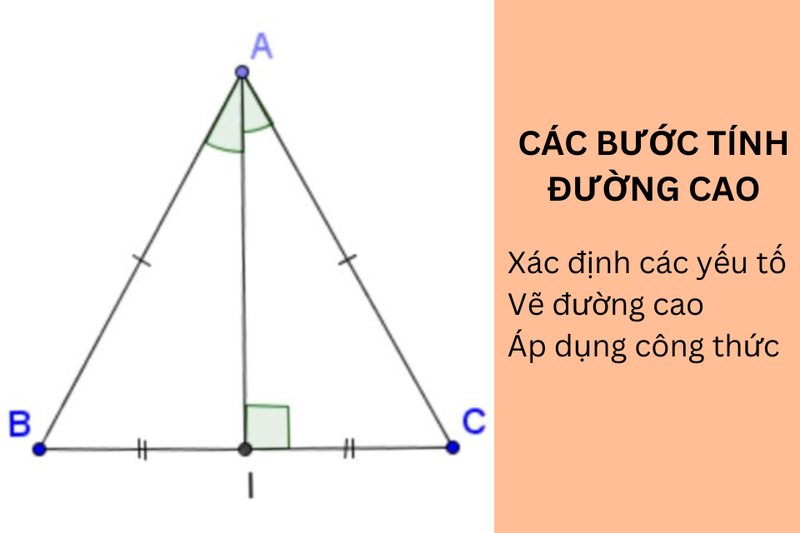
Trong tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường trung tuyến, đường trung trực và đường phân giác của góc ở đỉnh. Điều này có nghĩa là đường cao xuất phát từ đỉnh của tam giác cân xuống cạnh đáy sẽ chia đôi cạnh đáy, vuông góc với cạnh đáy, chia đôi góc ở đỉnh và là trục đối xứng của tam giác.

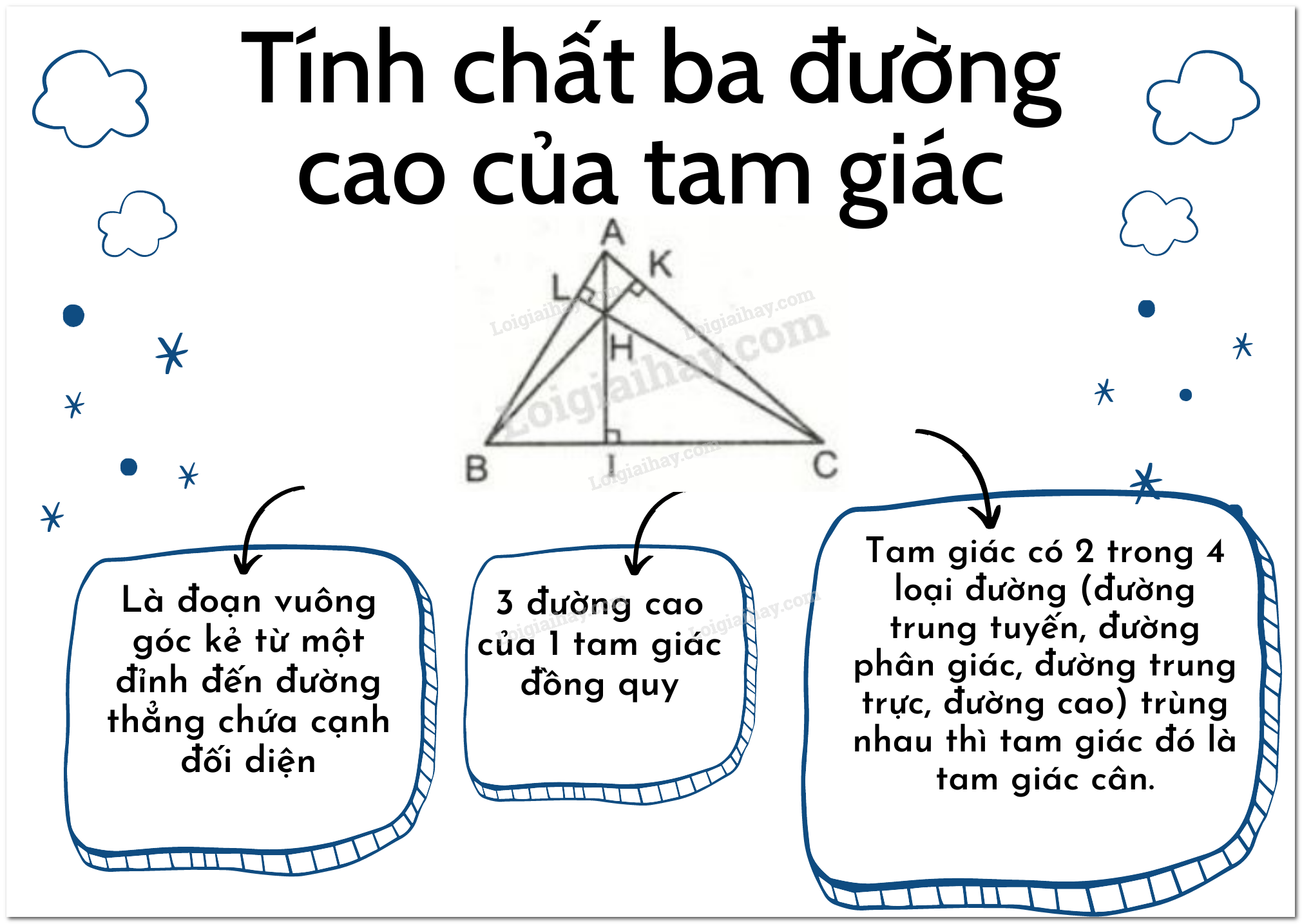
Chứng minh tính chất đường cao trong tam giác cân

Đường cao là đường trung tuyến

Xét tam giác cân ABC với AB = AC. Kẻ đường cao AH từ đỉnh A xuống cạnh đáy BC. Ta cần chứng minh BH = HC. Xét hai tam giác vuông AHB và AHC, ta có: AB = AC (giả thiết), AH chung. Theo định lý Pytago đảo, ta có BH = HC. Vậy đường cao AH cũng là đường trung tuyến.

Đường cao là đường trung trực

Vì đường cao AH chia đôi cạnh đáy BC (BH = HC) và vuông góc với BC tại H, nên AH là đường trung trực của BC.

Đường cao là đường phân giác

Xét hai tam giác vuông AHB và AHC. Ta có AB = AC (giả thiết), AH chung, BH = HC (đã chứng minh). Do đó, tam giác AHB bằng tam giác AHC (c.c.c). Suy ra góc BAH = góc CAH. Vậy đường cao AH cũng là đường phân giác của góc BAC.

Ứng dụng tính chất đường cao trong tam giác cân

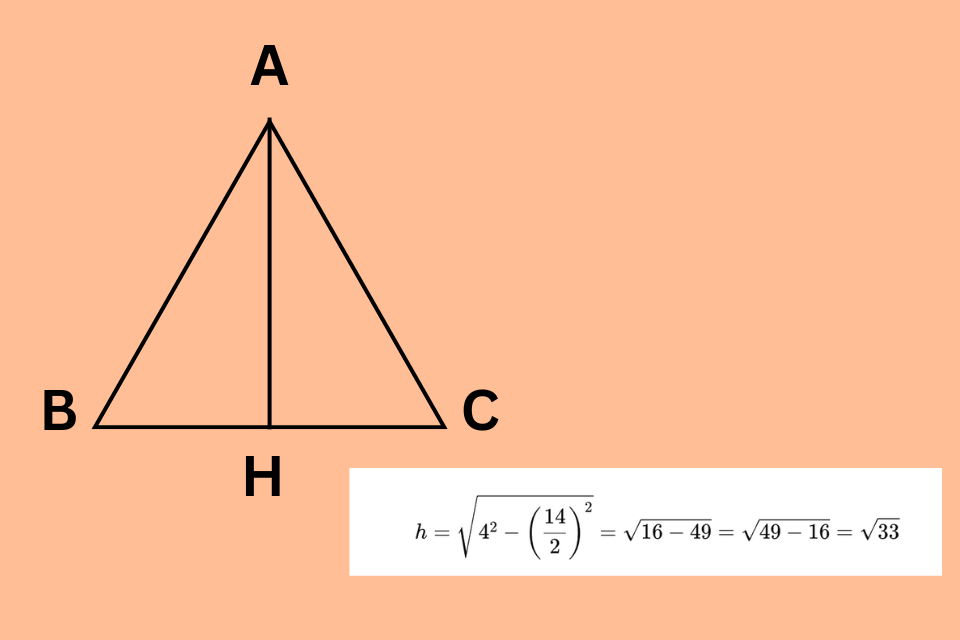
Tính chất đặc biệt này của đường cao trong tam giác cân được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là trong việc tính toán độ dài các cạnh, góc và diện tích của tam giác cân. Việc hiểu rõ tính chất này giúp giải quyết các bài toán một cách nhanh chóng và hiệu quả.

Xem thêm: cách làm giả cầy

Sản phẩm liên quan: lực đàn hồi là

Sản phẩm hữu ích: hướng dẫn ghép ngang b2

Sản phẩm liên quan: ăn gì để cương lâu