Diện tích tam giác đều lớp 12

Mô tả sản phẩm

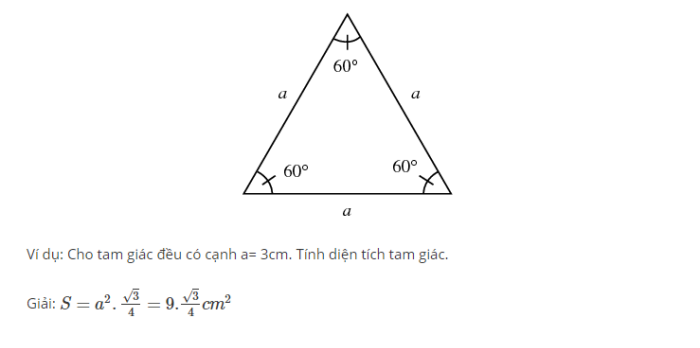
Diện tích tam giác đều được tính bằng công thức: S = (√3/4) * a², trong đó a là độ dài cạnh của tam giác đều. Đây là công thức quan trọng và thường được sử dụng trong chương trình toán lớp 12.

Công thức tính diện tích tam giác đều

Chứng minh công thức

Để chứng minh công thức S = (√3/4) * a², ta có thể sử dụng kiến thức về lượng giác. Chia tam giác đều thành hai tam giác vuông bằng nhau, mỗi tam giác có cạnh huyền là a và hai cạnh góc vuông là a/2 và h (chiều cao). Áp dụng định lý Pytago, ta có h² + (a/2)² = a². Từ đó suy ra h = (√3/2) * a. Diện tích tam giác đều bằng (1/2) * a * h = (1/2) * a * ((√3/2) * a) = (√3/4) * a².

Ví dụ minh họa

Cho một tam giác đều có cạnh a = 6cm. Diện tích tam giác đều này là: S = (√3/4) * 6² = (√3/4) * 36 = 9√3 cm².

Ứng dụng của công thức diện tích tam giác đều

Công thức tính diện tích tam giác đều được ứng dụng rộng rãi trong nhiều lĩnh vực, từ giải toán hình học phẳng đến các bài toán thực tế liên quan đến thiết kế, xây dựng… Việc nắm vững công thức và cách chứng minh nó là rất quan trọng đối với học sinh lớp 12.

Sản phẩm hữu ích: hợp chất ion là gì

Sản phẩm liên quan: sin bình 2x hạ bậc

Sản phẩm hữu ích: đề tiếng anh lớp 3 giữa kì 1

Sản phẩm liên quan: tỉ khối hơi là gì

Xem thêm: nhà nở hậu chữ l