Công thức hạ bậc sin bình 2x

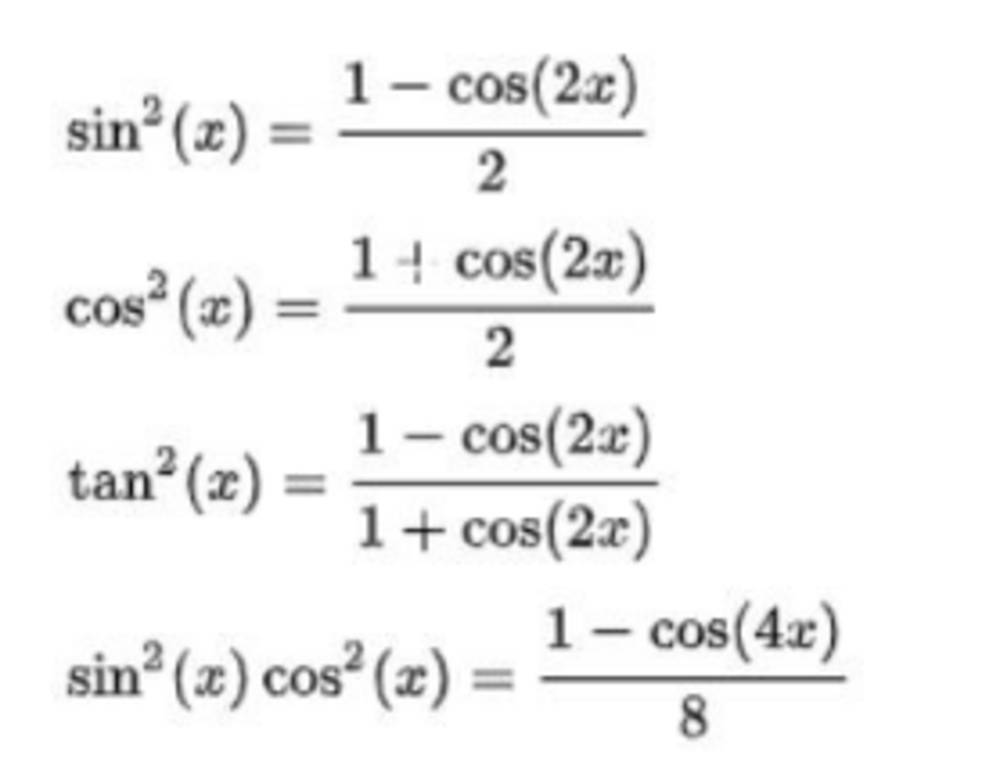
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức hạ bậc sin bình 2x được sử dụng để biến đổi biểu thức lượng giác phức tạp thành dạng đơn giản hơn, dễ tính toán. Công thức này dựa trên công thức lượng giác cơ bản và giúp giải quyết các bài toán tích phân, phương trình lượng giác... một cách hiệu quả. Cụ thể, ta có: sin²2x = (1 - cos4x)/2
Công thức hạ bậc sin bình 2x chi tiết
Từ công thức lượng giác cơ bản
Chúng ta bắt đầu từ công thức lượng giác cơ bản: cos2α = 1 - 2sin²α. Từ đây, ta có thể biểu diễn sin²α qua cos2α: sin²α = (1 - cos2α)/2. Áp dụng công thức này với α = 2x, ta thu được:
sin²2x = (1 - cos(2 * 2x))/2 = (1 - cos4x)/2
Ứng dụng của công thức hạ bậc sin bình 2x
Công thức này có nhiều ứng dụng trong giải tích và lượng giác, đặc biệt trong việc giải các phương trình lượng giác phức tạp, tính tích phân chứa hàm lượng giác, đơn giản hóa biểu thức lượng giác trước khi tính toán.
Ví dụ minh họa
Giả sử ta cần tính tích phân ∫sin²2x dx. Sử dụng công thức hạ bậc, ta có:
∫sin²2x dx = ∫(1 - cos4x)/2 dx = (1/2)∫(1 - cos4x) dx = (1/2)(x - (1/4)sin4x) + C
trong đó C là hằng số tích phân.
Lưu ý khi sử dụng công thức
Cần chú ý đến điều kiện xác định của các hàm lượng giác khi áp dụng công thức. Việc hiểu rõ các công thức lượng giác cơ bản là nền tảng để hiểu và sử dụng thành thạo công thức hạ bậc sin bình 2x.
Sản phẩm hữu ích: cách xóa gạch chân trong word
Xem thêm: cá diêu hồng kho thơm
Xem thêm: đơn vị của nhiệt lượng là gì