Công thức tính tất cả các hình

Mô tả sản phẩm

Không có một công thức duy nhất để tính "tất cả các hình" vì khái niệm "tất cả các hình" quá rộng và mơ hồ. Để tính toán diện tích, chu vi hay thể tích của một hình, bạn cần biết loại hình đó là gì. Mỗi hình học đều có công thức riêng. Bài viết này sẽ cung cấp một số công thức tính diện tích và chu vi của các hình học phổ biến.

Các hình học phẳng

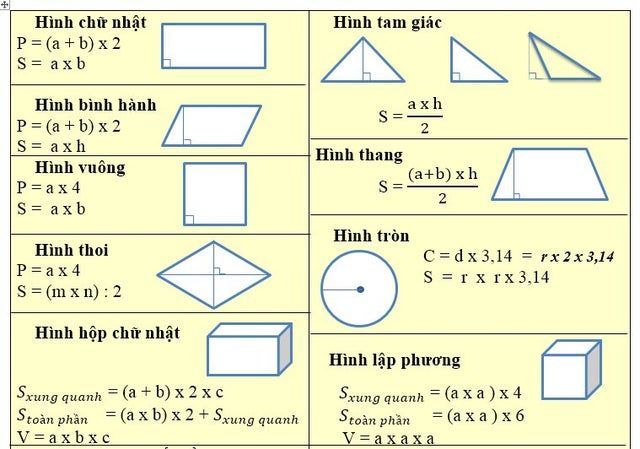
Hình chữ nhật

Diện tích: S = a x b (a là chiều dài, b là chiều rộng)
Chu vi: P = 2 x (a + b)

Hình vuông

Diện tích: S = a² (a là cạnh)
Chu vi: P = 4 x a

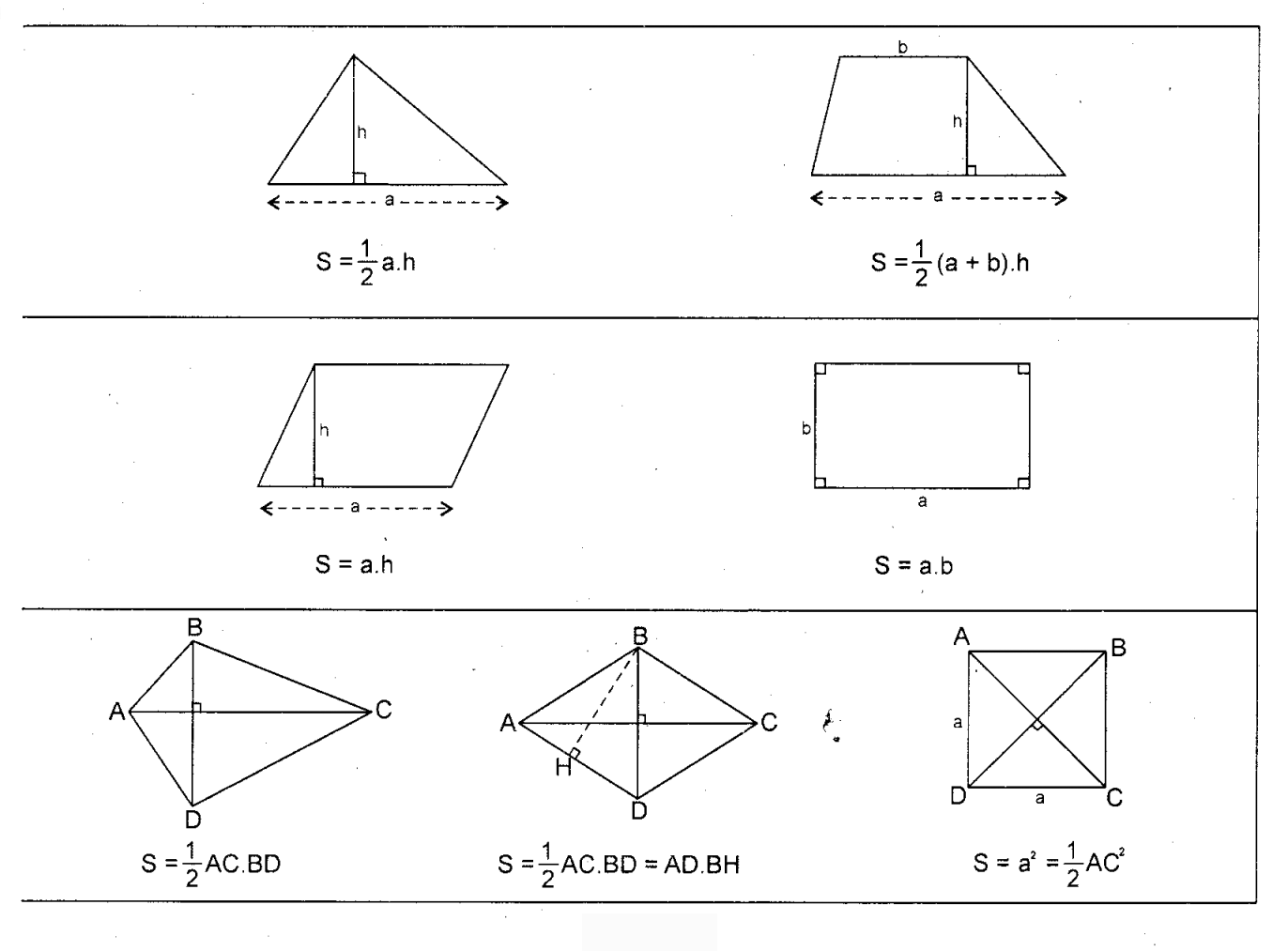
Hình tam giác

Diện tích: S = (a x h) / 2 (a là đáy, h là chiều cao)
Chu vi: P = a + b + c (a, b, c là ba cạnh)

Hình tròn

Diện tích: S = π x r² (r là bán kính, π ≈ 3.14159)
Chu vi: P = 2 x π x r

Các hình học không gian

Hình lập phương

Thể tích: V = a³ (a là cạnh)
Diện tích toàn phần: S = 6 x a²

Hình hộp chữ nhật

Thể tích: V = a x b x c (a, b, c là ba chiều)
Diện tích toàn phần: S = 2 x (ab + bc + ac)

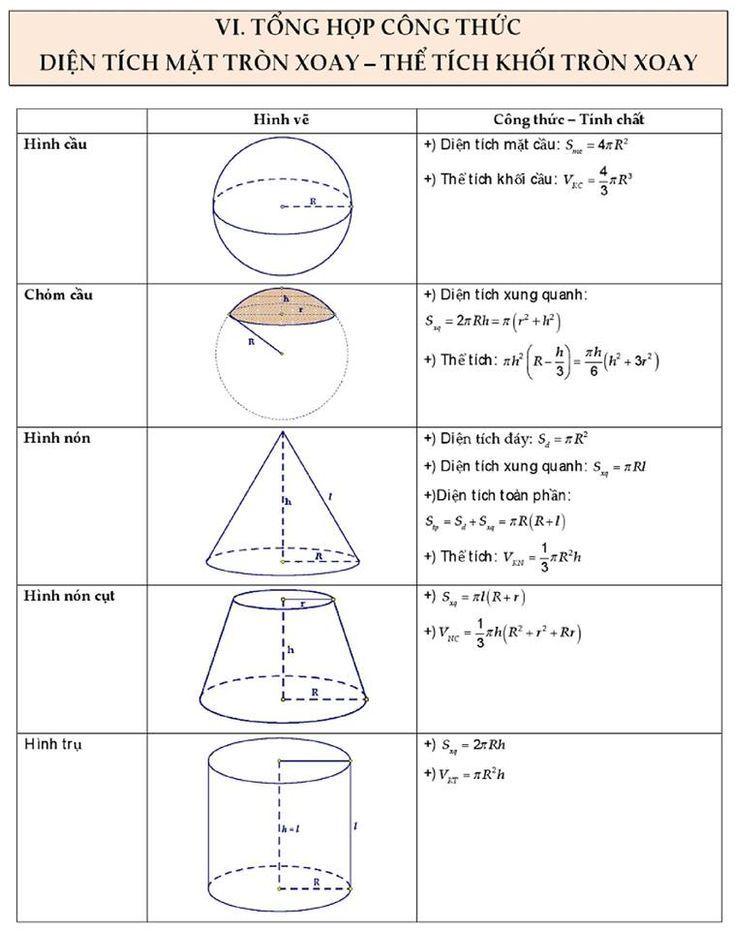
Hình cầu

Thể tích: V = (4/3) x π x r³ (r là bán kính)
Diện tích mặt cầu: S = 4 x π x r² Để tính toán cho các hình học phức tạp hơn, bạn cần sử dụng các phương pháp tích phân hoặc các công cụ toán học chuyên dụng. Hãy nhớ chỉ rõ loại hình bạn cần tính toán để có thể tìm được công thức chính xác.

Xem thêm: glucozo + br2

Sản phẩm liên quan: cứu tinh nàng thiên nga trọn bộ thuyết minh

Xem thêm: apa yang dapat kita lakukan untuk mengurangi penggunaan cfc dalam kehidupan sehari-hari

Sản phẩm hữu ích: sự điều tiết của mắt là gì

Xem thêm: trục đối xứng của parabol