Công thức tính lũy thừa lớp 6
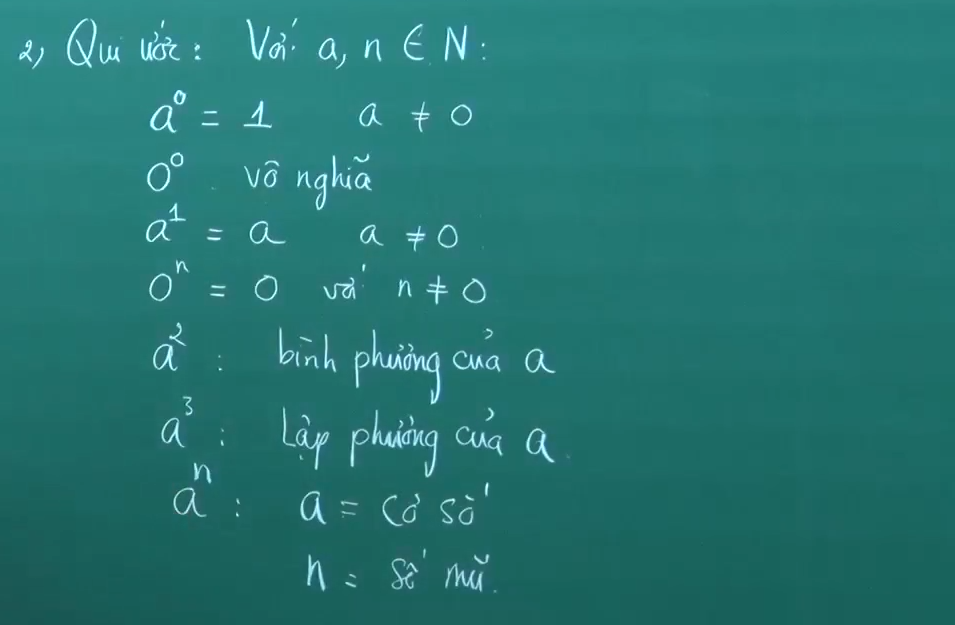


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính lũy thừa lớp 6 cơ bản là: am = a × a × ... × a (m thừa số a), trong đó a là cơ số và m là số mũ (m là số tự nhiên khác 0). Ví dụ: 23 = 2 × 2 × 2 = 8.
Các trường hợp đặc biệt của lũy thừa
Lũy thừa với số mũ 0
Với bất kì số tự nhiên a khác 0, ta luôn có a0 = 1. Ví dụ: 50 = 1, 100 = 1. Lưu ý rằng 00 không xác định.Lũy thừa với số mũ 1
Với bất kì số tự nhiên a nào, ta luôn có a1 = a. Ví dụ: 31 = 3, 1001 = 100.Lũy thừa của 10
Lũy thừa của 10 có dạng 10m (với m là số tự nhiên) sẽ có kết quả là số 1 với m chữ số 0. Ví dụ: 102 = 100, 105 = 100000. Đây là một công thức đặc biệt hữu ích để hiểu về hệ thập phân.Quy tắc tính toán lũy thừa
Ngoài công thức cơ bản, khi tính toán lũy thừa, ta cần lưu ý đến các quy tắc sau:- Nhân hai lũy thừa cùng cơ số: am × an = am+n (Ví dụ: 23 × 22 = 23+2 = 25 = 32)
- Chia hai lũy thừa cùng cơ số: am : an = am-n (với a ≠ 0 và m ≥ n) (Ví dụ: 25 : 22 = 25-2 = 23 = 8)
- Lũy thừa của một lũy thừa: (am)n = am×n (Ví dụ: (23)2 = 23×2 = 26 = 64)
- Lũy thừa của một tích: (a × b)m = am × bm (Ví dụ: (2 × 3)2 = 22 × 32 = 4 × 9 = 36)
- Lũy thừa của một thương: (a : b)m = am : bm (với b ≠ 0) (Ví dụ: (6:2)2 = 62 : 22 = 36:4 = 9)
Sản phẩm liên quan: cách đổi từ km sang m
Sản phẩm hữu ích: công thức đường tròn ngoại tiếp
Sản phẩm hữu ích: giá trị tuyệt đối của x