Công thức Đường Tròn Ngoại Tiếp

Mô tả sản phẩm

Công thức đường tròn ngoại tiếp được sử dụng để tính bán kính và tâm của đường tròn ngoại tiếp một tam giác. Bán kính đường tròn ngoại tiếp phụ thuộc vào độ dài các cạnh của tam giác hoặc các yếu tố khác như diện tích và chu vi.

Công thức tính bán kính đường tròn ngoại tiếp

Công thức dựa trên độ dài cạnh và diện tích

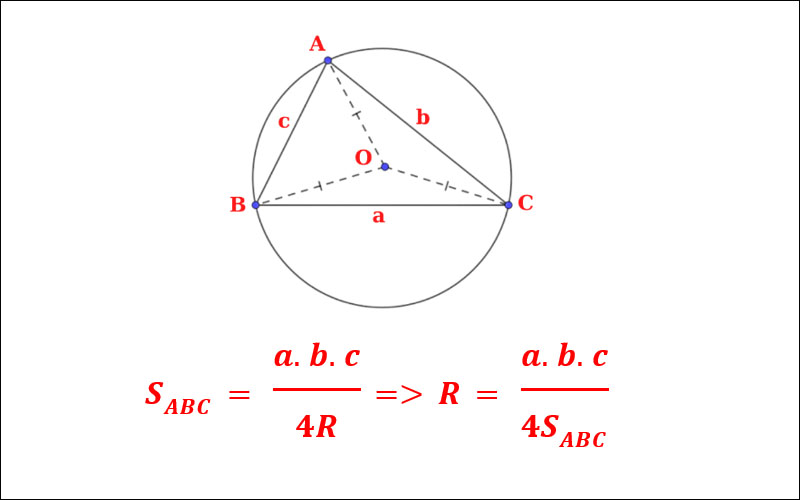
Công thức tổng quát tính bán kính R của đường tròn ngoại tiếp tam giác ABC với a, b, c là độ dài các cạnh và S là diện tích tam giác:
R = abc / 4S
Trong đó:
a, b, c là độ dài các cạnh của tam giác.
S là diện tích của tam giác. Diện tích S có thể tính bằng công thức Heron: S = √[p(p-a)(p-b)(p-c)], với p là nửa chu vi tam giác (p = (a+b+c)/2).

Công thức dựa trên định lý sin

Một cách khác để tính bán kính R là sử dụng định lý sin:
R = a / 2sinA = b / 2sinB = c / 2sinC
Trong đó:
A, B, C là các góc của tam giác.
a, b, c là độ dài các cạnh đối diện với các góc A, B, C tương ứng.

Trường hợp đặc biệt: Tam giác vuông

Với tam giác vuông, bán kính đường tròn ngoại tiếp bằng một nửa độ dài cạnh huyền. Nếu cạnh huyền là c, thì R = c/2.

Tìm tâm đường tròn ngoại tiếp

Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của các cạnh tam giác. Việc xác định tọa độ tâm thường được thực hiện thông qua hệ phương trình dựa trên các phương trình đường trung trực.

Ví dụ minh họa

Giả sử ta có một tam giác với các cạnh a = 3, b = 4, c = 5 (tam giác vuông). Diện tích S = (1/2)*3*4 = 6. Áp dụng công thức R = abc / 4S, ta có R = (3*4*5) / (4*6) = 2.5. Như vậy, bán kính đường tròn ngoại tiếp tam giác này là 2.5. Điều này khớp với công thức cho tam giác vuông (R = c/2 = 5/2 = 2.5).

Sản phẩm liên quan: cách đổi đơn vị mét khối

Sản phẩm liên quan: pha nước chấm ốc luộc

Sản phẩm liên quan: câu đố toán học cho học sinh tiểu học

Sản phẩm hữu ích: yếu tố khách quan thúc đẩy sự ra đời của tổ chức asean