Công Thức Hình Học 12

Mô tả sản phẩm

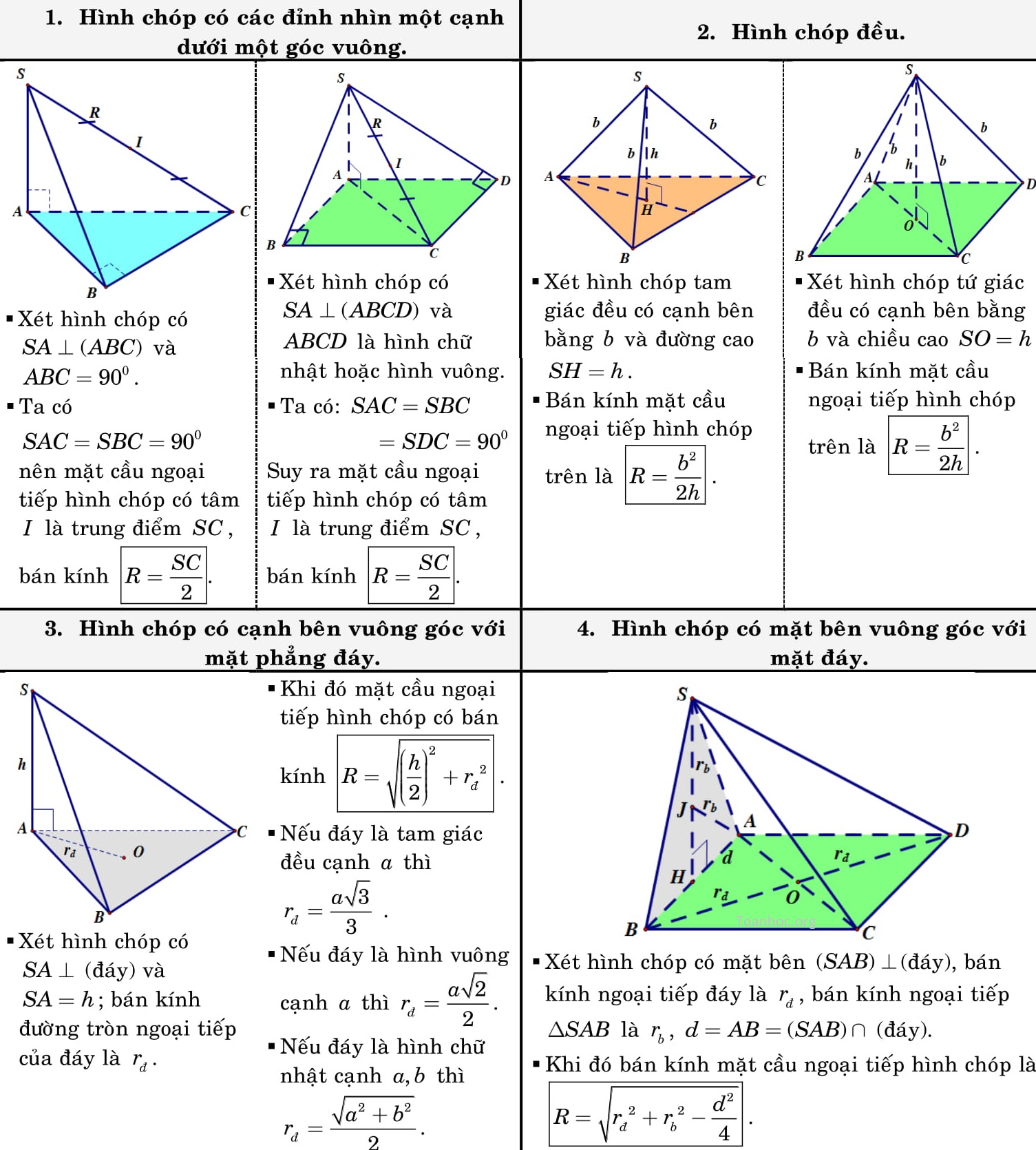
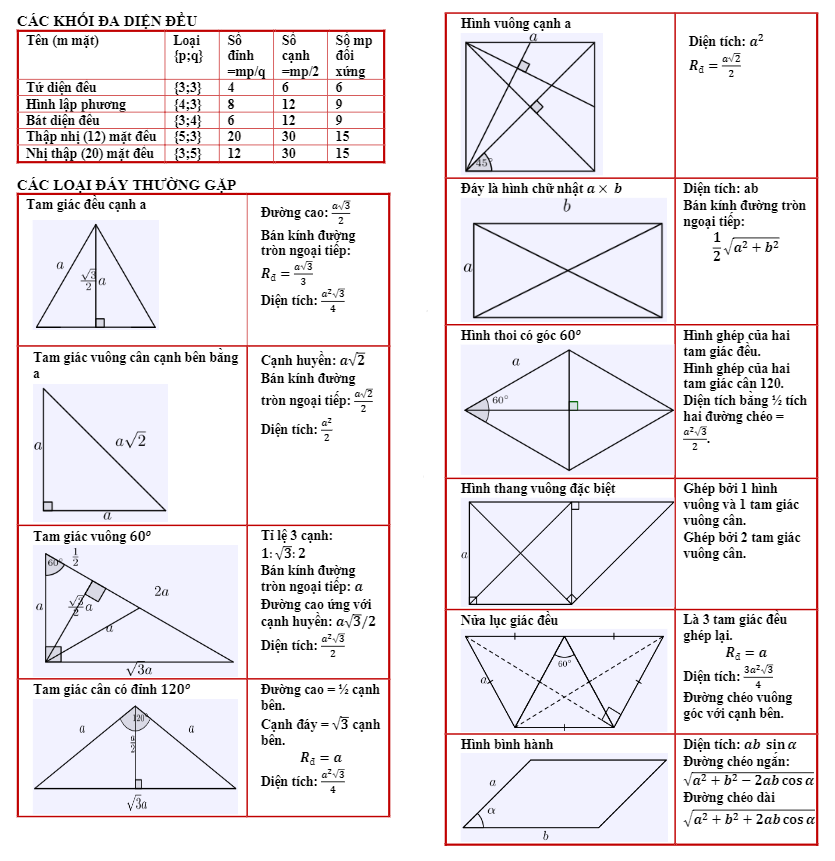
Bạn đang tìm kiếm công thức hình học lớp 12? Bài viết này sẽ tổng hợp đầy đủ các công thức quan trọng và cần thiết trong chương trình Hình học 12, giúp bạn ôn tập và làm bài tập hiệu quả hơn. Chúng tôi sẽ chia sẻ các công thức liên quan đến hình học không gian, bao gồm hình chóp, hình lăng trụ, hình cầu, hình nón và các công thức tính diện tích, thể tích của chúng.

Hình Học Không Gian

Hình Chóp

Công thức tính thể tích hình chóp: V = (1/3) * S * h, trong đó S là diện tích đáy và h là chiều cao. Công thức tính diện tích xung quanh của hình chóp đều: Sxq = (1/2) * p * l, với p là nửa chu vi đáy và l là độ dài cạnh bên.

Hình Lăng Trụ

Công thức tính thể tích hình lăng trụ: V = S * h, trong đó S là diện tích đáy và h là chiều cao. Công thức tính diện tích xung quanh của hình lăng trụ đứng: Sxq = 2 * p * h, với p là chu vi đáy và h là chiều cao.

Hình Cầu

Công thức tính thể tích hình cầu: V = (4/3) * π * R³, với R là bán kính hình cầu. Công thức tính diện tích mặt cầu: S = 4 * π * R².

Hình Nón

Công thức tính thể tích hình nón: V = (1/3) * π * R² * h, với R là bán kính đáy và h là chiều cao. Công thức tính diện tích xung quanh hình nón: Sxq = π * R * l, với l là độ dài đường sinh.

Ứng dụng thực tiễn của các công thức

Việc nắm vững các công thức hình học lớp 12 không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn rất hữu ích trong thực tiễn. Bạn có thể áp dụng các công thức này để tính toán thể tích, diện tích của các vật thể trong cuộc sống hàng ngày, hỗ trợ trong các lĩnh vực như kiến trúc, xây dựng, kỹ thuật…

Lưu ý

Hãy nhớ rằng việc hiểu rõ bản chất của từng công thức và cách áp dụng chúng vào các bài toán khác nhau mới là điều quan trọng nhất. Đừng chỉ học thuộc lòng mà hãy cố gắng hiểu sâu sắc để giải quyết được mọi bài toán một cách hiệu quả.

Sản phẩm liên quan: test trình độ tiếng việt

Sản phẩm liên quan: bộ phận hk là gì

Sản phẩm hữu ích: độ lớn lực ma sát

Sản phẩm hữu ích: quy tắc cộng, trừ số âm dương

Sản phẩm hữu ích: góc giữa 2 véc tơ