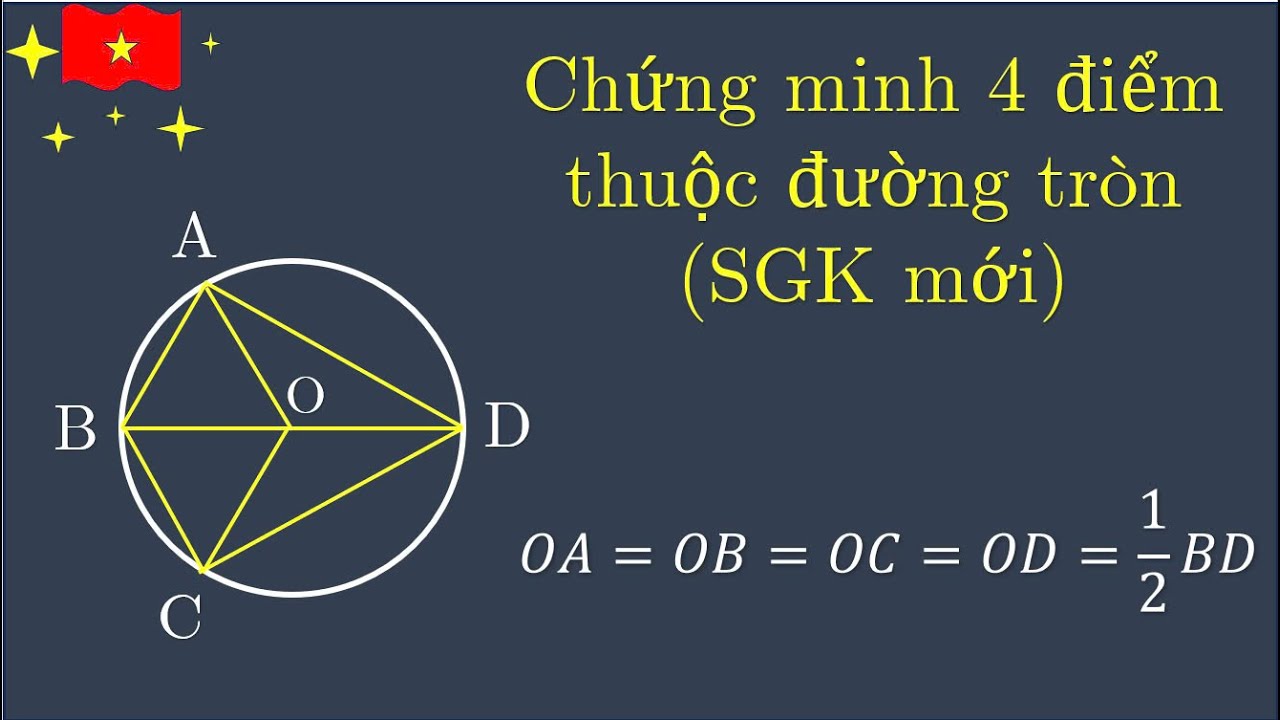
Chứng minh bốn điểm cùng thuộc một đường tròn

Mô tả sản phẩm

Để chứng minh bốn điểm cùng thuộc một đường tròn, ta cần chứng minh rằng các điểm đó thỏa mãn một trong các điều kiện sau: bốn điểm tạo thành một tứ giác nội tiếp, hoặc ba điểm tạo thành một tam giác và điểm thứ tư nằm trên đường tròn ngoại tiếp tam giác đó. Dưới đây là bốn phương pháp chứng minh phổ biến.

Phương pháp 1: Sử dụng góc nội tiếp

Điều kiện:

Tứ giác nội tiếp. Nếu các góc đối của một tứ giác có tổng bằng 180 độ, thì tứ giác đó nội tiếp đường tròn.

Chứng minh:

Giả sử tứ giác ABCD có góc A + góc C = 180° và góc B + góc D = 180°. Vẽ đường tròn đi qua ba điểm A, B, C. Nếu điểm D nằm ngoài đường tròn, thì góc nội tiếp ADC sẽ nhỏ hơn góc nội tiếp ABC (hoặc ngược lại nếu D nằm trong đường tròn). Điều này mâu thuẫn với giả thiết góc A + góc C = 180°. Do đó, điểm D phải nằm trên đường tròn đi qua A, B, C. Vậy bốn điểm A, B, C, D cùng thuộc một đường tròn.

Phương pháp 2: Sử dụng định lý Thales

Điều kiện:

Ba điểm thẳng hàng. Nếu một đường kính của đường tròn đi qua trung điểm của một dây cung, thì đường kính đó vuông góc với dây cung. Ngược lại, nếu một đường kính vuông góc với một dây cung, thì nó đi qua trung điểm của dây cung.

Chứng minh:

Giả sử ta có ba điểm A, B, C nằm trên đường tròn. Ta muốn chứng minh điểm D cũng nằm trên đường tròn đó. Nếu AB là đường kính và CD vuông góc với AB tại trung điểm M của CD, thì theo định lý Thales, điểm D sẽ nằm trên đường tròn đường kính AB.

Phương pháp 3: Sử dụng góc ở tâm và góc nội tiếp

Điều kiện:

Góc nội tiếp chắn cung. Góc nội tiếp bằng một nửa góc ở tâm cùng chắn một cung.

Chứng minh:

Giả sử ta có tam giác ABC nội tiếp đường tròn (O). Để chứng minh điểm D cũng thuộc đường tròn này, ta cần chứng minh góc ADB bằng góc ACB (hoặc góc ADC bằng góc ABC), khi đó góc ADB (hay ADC) là góc nội tiếp cùng chắn cung AB (hay AC).

Phương pháp 4: Sử dụng phương tích

Điều kiện:

Phương tích của một điểm đối với đường tròn. Phương tích của một điểm đối với một đường tròn là tích khoảng cách từ điểm đó đến hai giao điểm của đường tròn với một đường thẳng bất kì đi qua điểm đó.

Chứng minh:

Giả sử ta có ba điểm A, B, C thuộc đường tròn. Để chứng minh điểm D cùng thuộc đường tròn, ta cần chứng minh phương tích của điểm D đối với đường tròn đi qua A, B, C bằng 0. Điều này có nghĩa là điểm D nằm trên đường tròn.

Xem thêm: cách tìm tiêu điểm của parabol

Sản phẩm liên quan: cách để mắt không tăng độ cận thị

Sản phẩm hữu ích: cách pha b1 tưới cây

Xem thêm: chim hut mat hot

Sản phẩm hữu ích: kho bau rong vang