Chứng minh 4 điểm cùng thuộc một đường tròn

Mô tả sản phẩm

Để chứng minh 4 điểm cùng thuộc một đường tròn, ta cần chứng minh rằng tồn tại một đường tròn đi qua cả 4 điểm đó. Điều này có thể được thực hiện bằng cách sử dụng một trong các phương pháp sau: chứng minh tổng hai góc đối diện bằng 180 độ, chứng minh các điểm cùng nằm trên đường tròn có tâm và bán kính xác định, sử dụng định lý về góc nội tiếp hoặc tính chất của tứ giác nội tiếp.

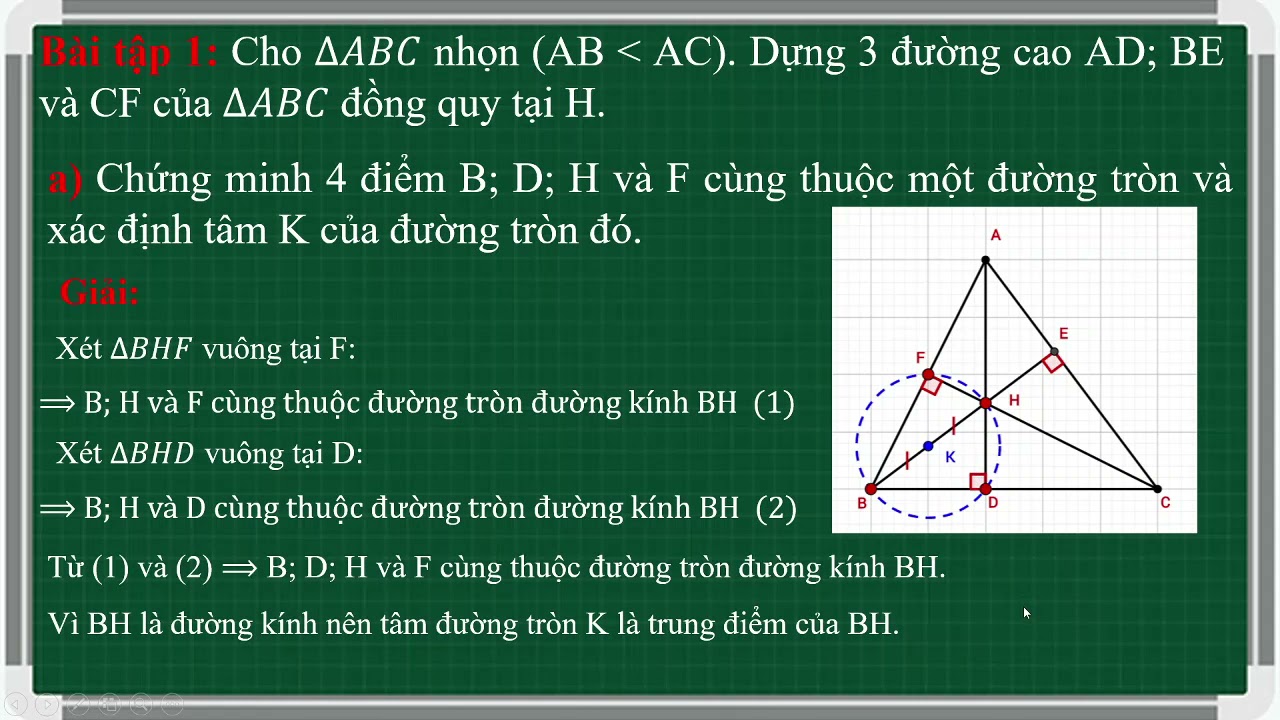
Các phương pháp chứng minh 4 điểm cùng thuộc một đường tròn

1. Sử dụng định lý về góc nội tiếp:

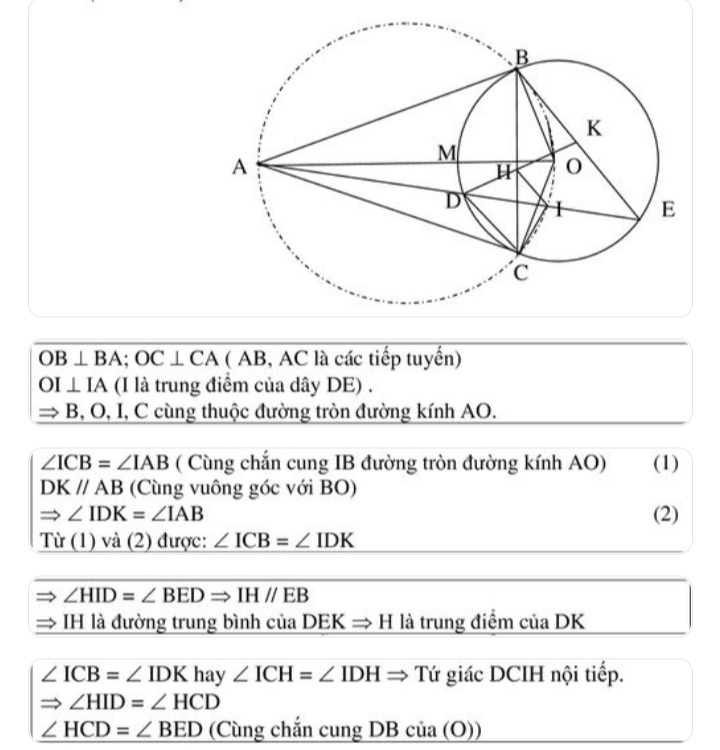
Nếu bốn điểm A, B, C, D cùng nằm trên một đường tròn, thì góc nội tiếp chắn cung AB bằng góc nội tiếp chắn cung CD. Hay nói cách khác, nếu góc nội tiếp ∠ADB = ∠ACB thì bốn điểm A, B, C, D cùng thuộc một đường tròn. Phương pháp này thường được sử dụng khi ta đã biết mối quan hệ giữa các góc trong hình.

2. Chứng minh tứ giác nội tiếp:

Một tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên cùng một đường tròn. Để chứng minh một tứ giác ABCD nội tiếp, ta có thể sử dụng các điều kiện sau:

• Tổng hai góc đối diện bằng 180 độ: ∠ABC + ∠ADC = 180° (hoặc ∠BAD + ∠BCD = 180°)
• Hai góc nội tiếp cùng chắn một cung bằng nhau.
• Góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn cung đó.

Nếu thỏa mãn một trong các điều kiện trên, thì tứ giác ABCD nội tiếp, do đó bốn điểm A, B, C, D cùng thuộc một đường tròn. Đây là phương pháp được sử dụng rộng rãi và hiệu quả.

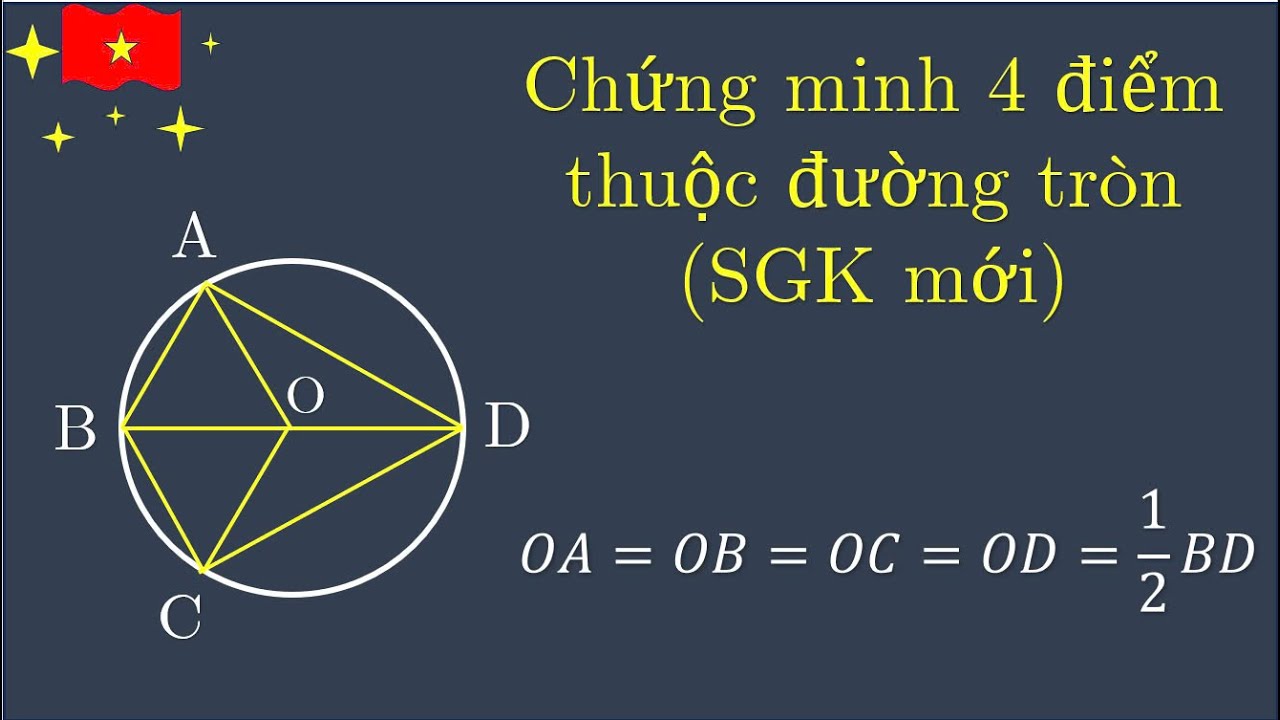
3. Xác định tâm và bán kính của đường tròn:

Nếu ta tìm được một điểm O sao cho OA = OB = OC = OD (khoảng cách từ O đến bốn điểm A, B, C, D bằng nhau), thì bốn điểm A, B, C, D cùng thuộc đường tròn tâm O, bán kính OA. Phương pháp này thường khó áp dụng hơn hai phương pháp trên, đặc biệt trong các bài toán phức tạp.

4. Sử dụng hệ thức lượng trong tam giác:

Trong một số trường hợp, ta có thể sử dụng hệ thức lượng trong tam giác để chứng minh 4 điểm cùng thuộc một đường tròn. Ví dụ, nếu ta chứng minh được rằng tích hai đoạn thẳng cắt nhau bằng tích hai đoạn thẳng còn lại (định lý Ptoleme), thì tứ giác đó nội tiếp, và do đó 4 điểm cùng nằm trên một đường tròn. Tóm lại, có nhiều cách để chứng minh 4 điểm cùng thuộc một đường tròn. Việc lựa chọn phương pháp phụ thuộc vào dữ kiện bài toán cụ thể. Hiểu rõ các phương pháp này sẽ giúp bạn giải quyết hiệu quả các bài toán hình học phức tạp.

Xem thêm: phương trình chuyển động rơi tự do

Sản phẩm liên quan: cách bấm phân số trên máy tính

Sản phẩm hữu ích: cách chứng minh 4 điểm thuộc đường tròn

Xem thêm: cách quét vôi tường

Xem thêm: dua con toi loi