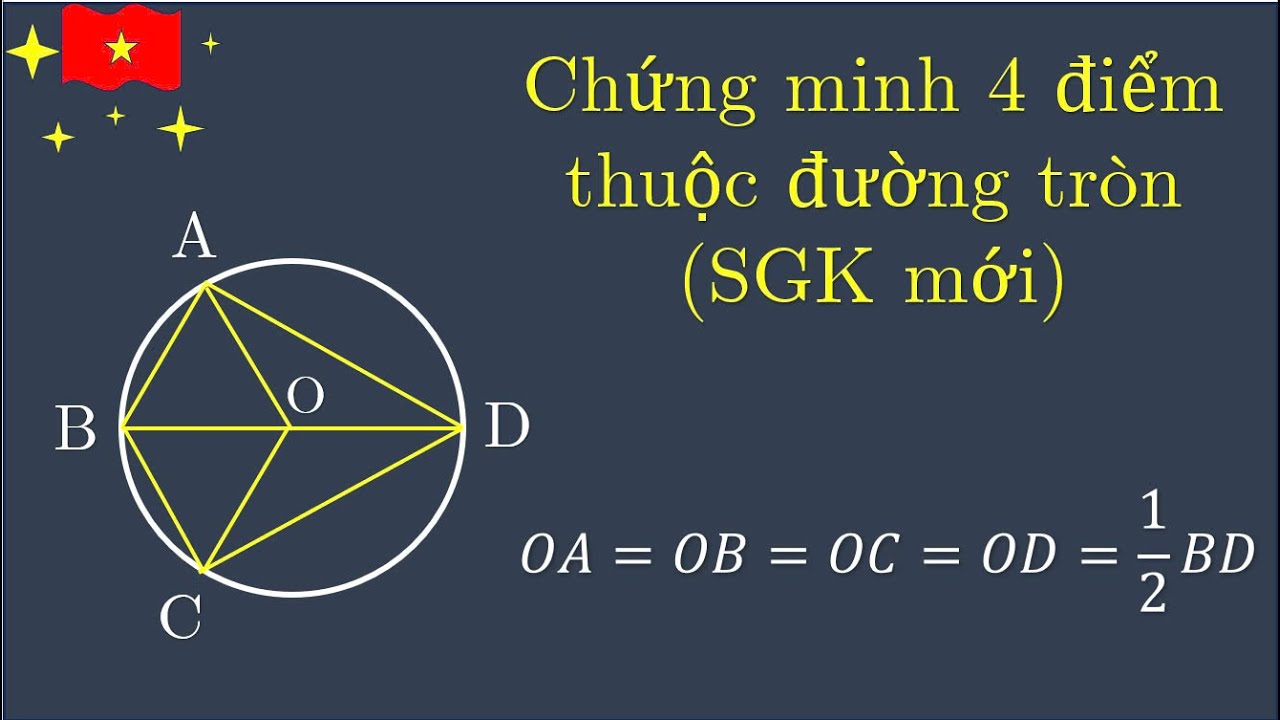
Cách Chứng Minh 4 Điểm Thuộc Đường Tròn

Mô tả sản phẩm

Bạn muốn biết cách chứng minh 4 điểm cùng nằm trên một đường tròn? Có nhiều phương pháp để chứng minh điều này, tùy thuộc vào thông tin đã biết về các điểm đó. Bài viết này sẽ hướng dẫn bạn một số cách phổ biến và hiệu quả nhất.

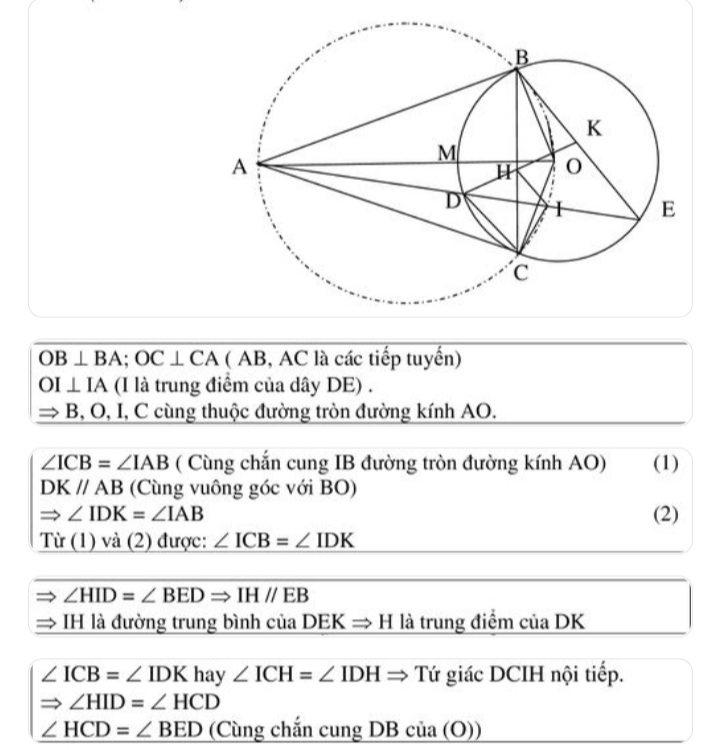
Phương pháp 1: Sử dụng định lý về góc nội tiếp

Định lý góc nội tiếp là gì?

Định lý góc nội tiếp phát biểu rằng: Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau. Ngược lại, nếu hai góc nội tiếp cùng chắn một cung và bằng nhau thì bốn điểm tạo thành tứ giác nội tiếp.

Áp dụng để chứng minh 4 điểm thuộc đường tròn:

Để chứng minh 4 điểm A, B, C, D thuộc đường tròn, ta cần chứng minh hai góc nội tiếp cùng chắn một cung bằng nhau. Ví dụ: Chứng minh rằng ∠ABC = ∠ADC (hoặc ∠BAD = ∠BCD). Nếu điều này được chứng minh, thì bốn điểm A, B, C, D cùng nằm trên một đường tròn.

Phương pháp 2: Sử dụng định lý Ptolemy

Định lý Ptolemy là gì?

Định lý Ptolemy phát biểu rằng: Trong một tứ giác nội tiếp, tích của hai đường chéo bằng tổng tích của hai cặp cạnh đối diện. Ngược lại, nếu trong một tứ giác, tích của hai đường chéo bằng tổng tích của hai cặp cạnh đối diện thì tứ giác đó nội tiếp.

Áp dụng để chứng minh 4 điểm thuộc đường tròn:

Cho tứ giác ABCD. Nếu ta chứng minh được AC.BD = AB.CD + BC.AD, thì tứ giác ABCD nội tiếp, hay nói cách khác, bốn điểm A, B, C, D cùng nằm trên một đường tròn.

Phương pháp 3: Sử dụng tọa độ

Sử dụng phương trình đường tròn:

Nếu biết tọa độ của bốn điểm A, B, C, D, ta có thể tìm phương trình đường tròn đi qua ba điểm bất kỳ trong số bốn điểm đó (ví dụ A, B, C). Sau đó, ta thay tọa độ điểm D vào phương trình đường tròn đó. Nếu tọa độ điểm D thỏa mãn phương trình, thì điểm D cũng nằm trên đường tròn, và do đó, bốn điểm A, B, C, D cùng nằm trên một đường tròn.

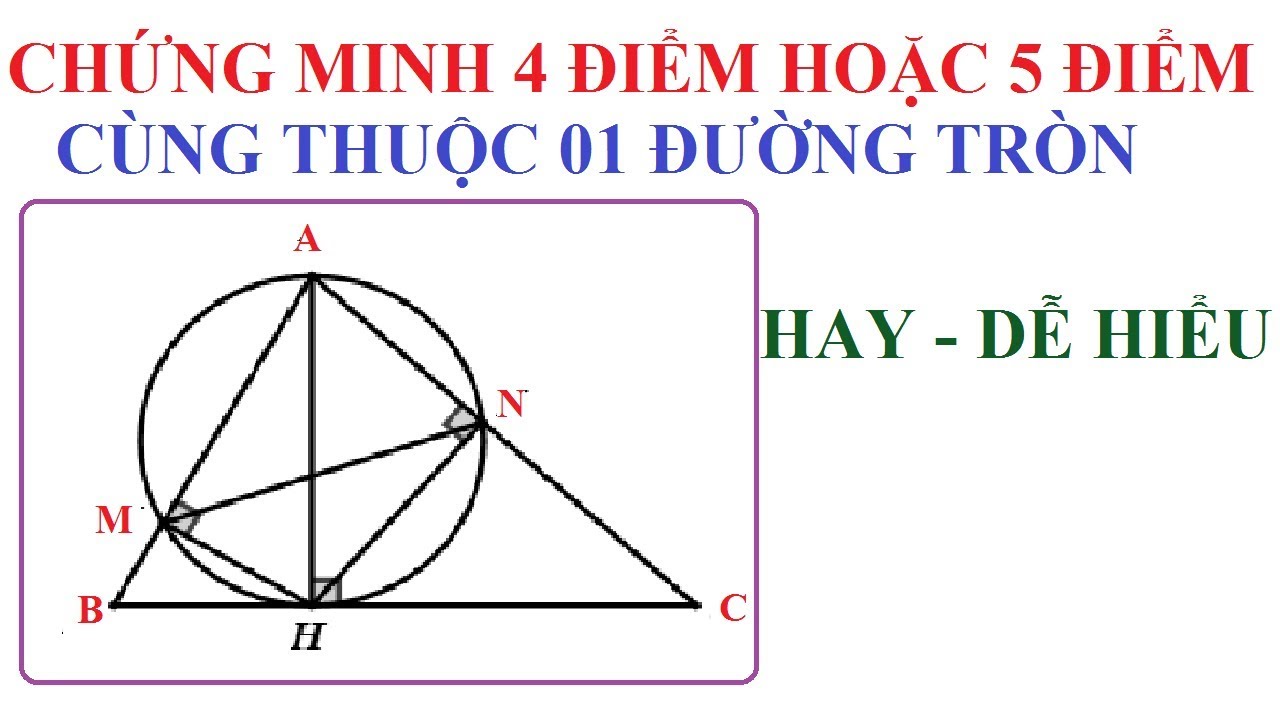
Phương pháp 4: Sử dụng tính chất đường tròn ngoại tiếp

Đường tròn ngoại tiếp tam giác:

Xét ba điểm A, B, C bất kỳ không thẳng hàng. Luôn tồn tại một đường tròn duy nhất đi qua ba điểm này, đó là đường tròn ngoại tiếp tam giác ABC. Nếu điểm D cũng nằm trên đường tròn ngoại tiếp tam giác ABC, thì bốn điểm A, B, C, D cùng nằm trên một đường tròn.

Sản phẩm hữu ích: axit có những khả năng nào

Xem thêm: cách vẽ búp be giấy đơn giản nhất

Xem thêm: hóa chất thí nghiệm