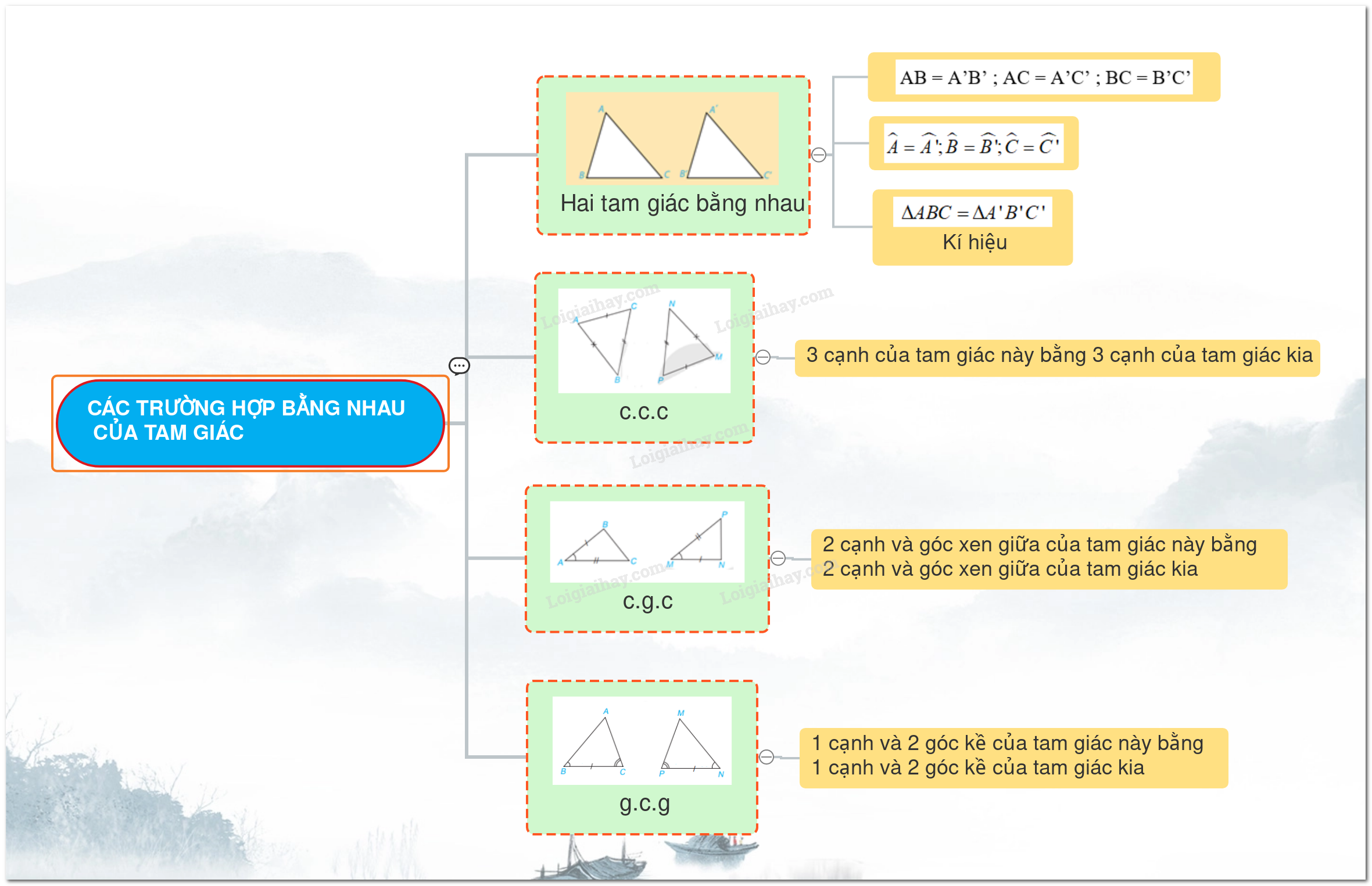
Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Mô tả sản phẩm

Trường hợp bằng nhau thứ hai của tam giác là trường hợp hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia. Trường hợp bằng nhau thứ ba là trường hợp cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia.

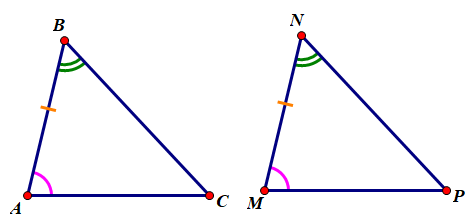
Trường hợp bằng nhau thứ hai (c.g.c)

Điều kiện áp dụng:

Hai tam giác được gọi là bằng nhau theo trường hợp cạnh - góc - cạnh (c.g.c) nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia.

Ví dụ minh họa:

Cho tam giác ABC và tam giác DEF. Nếu AB = DE, ∠A = ∠D, AC = DF thì ∆ABC = ∆DEF (c.g.c).

Trường hợp bằng nhau thứ ba (ch-cgv)

Điều kiện áp dụng:

Hai tam giác vuông được gọi là bằng nhau theo trường hợp cạnh huyền - cạnh góc vuông (ch-cgv) nếu cạnh huyền và một cạnh góc vuông của tam giác này bằng cạnh huyền và một cạnh góc vuông của tam giác kia.

Ví dụ minh họa:

Cho hai tam giác vuông ABC (vuông tại A) và DEF (vuông tại D). Nếu BC = EF (cạnh huyền) và AC = DF (cạnh góc vuông) thì ∆ABC = ∆DEF (ch-cgv).

Lưu ý: Chỉ áp dụng trường hợp này cho tam giác vuông. Không thể áp dụng cho tam giác thường.

Tóm lại, để chứng minh hai tam giác bằng nhau, ta cần xem xét xem chúng thỏa mãn trường hợp bằng nhau nào trong ba trường hợp: cạnh - cạnh - cạnh (c.c.c), cạnh - góc - cạnh (c.g.c) hay cạnh huyền - cạnh góc vuông (ch-cgv) (cho tam giác vuông).

Xem thêm: rẻ rách mà cứ nghĩ mình là

Sản phẩm liên quan: cây táo ra quả vào mùa nào

Sản phẩm liên quan: gạo tiếng nhật là gì