Trực Tâm Tam Giác Đều

Mô tả sản phẩm

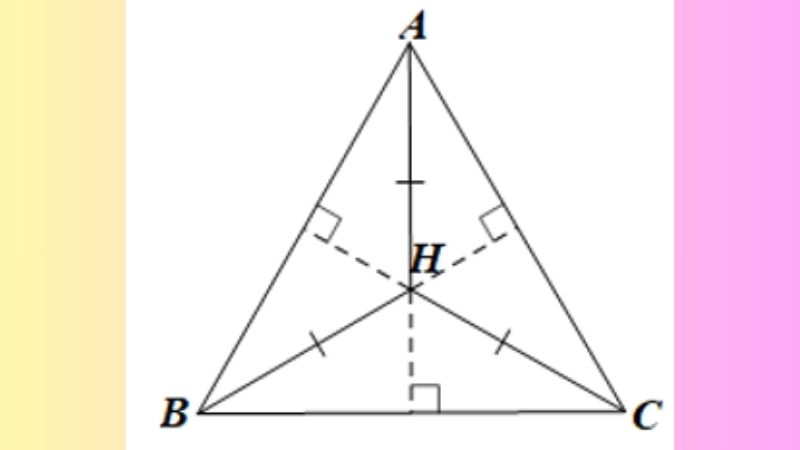
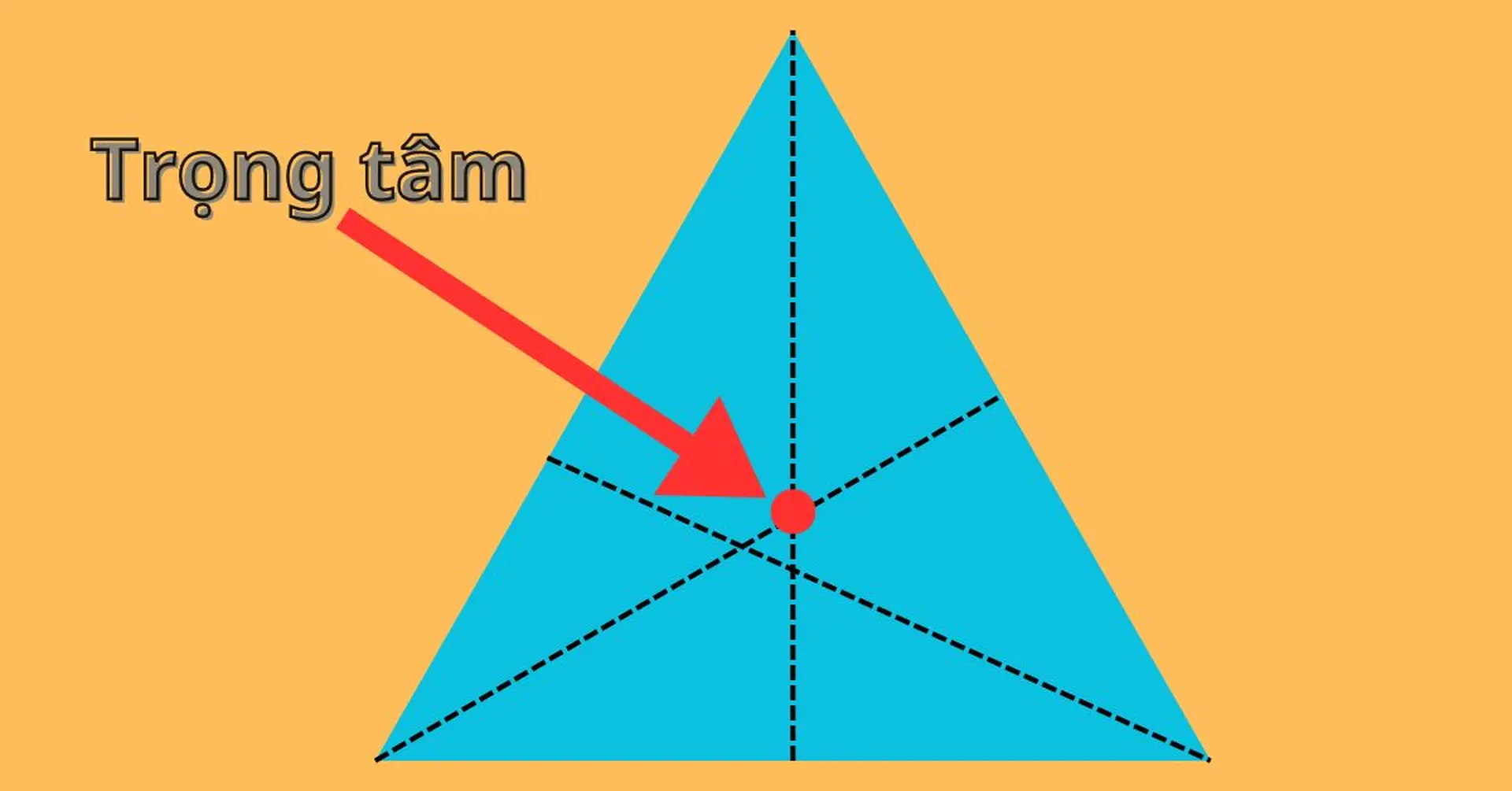
Trực tâm của tam giác đều chính là giao điểm của ba đường cao, đồng thời cũng là giao điểm của ba đường trung tuyến, ba đường trung trực và ba đường phân giác. Nói cách khác, trực tâm của tam giác đều trùng với trọng tâm của tam giác đó.

Vị trí của trực tâm trong tam giác đều

Tính chất đặc biệt

Trong một tam giác đều, ba đường cao, ba đường trung tuyến, ba đường trung trực và ba đường phân giác đều trùng nhau và đồng quy tại một điểm. Điểm này chính là trực tâm của tam giác đều, và nó cũng chính là trọng tâm của tam giác. Điều này dẫn đến một số tính chất đặc biệt: Khoảng cách từ trực tâm đến mỗi đỉnh bằng 2/3 chiều dài đường cao. Khoảng cách từ trực tâm đến mỗi cạnh bằng 1/3 chiều dài đường cao.

Cách xác định trực tâm tam giác đều

Phương pháp thực hành

Để xác định trực tâm của một tam giác đều, bạn có thể sử dụng bất kỳ phương pháp nào sau đây:

• Vẽ ba đường cao: Vẽ ba đường thẳng vuông góc với mỗi cạnh và đi qua đỉnh đối diện. Giao điểm của ba đường cao này chính là trực tâm.
• Vẽ ba đường trung tuyến: Vẽ ba đoạn thẳng nối mỗi đỉnh với trung điểm của cạnh đối diện. Giao điểm của ba đường trung tuyến này chính là trực tâm (và cũng là trọng tâm).
• Sử dụng công thức tọa độ (nếu biết tọa độ các đỉnh): Với tam giác đều ABC có tọa độ A, B, C, bạn có thể sử dụng công thức tính tọa độ trọng tâm (cũng là trực tâm) G = ((xA + xB + xC)/3, (yA + yB + yC)/3).

Như vậy, việc tìm trực tâm của tam giác đều trở nên đơn giản hơn nhiều so với các loại tam giác khác nhờ tính đối xứng đặc biệt của nó.

Sản phẩm hữu ích: câu đố về hiện tượng tự nhiên

Sản phẩm hữu ích: điều kiện phản ứng

Sản phẩm hữu ích: sinh lý học là gì