Tọa độ các tiêu điểm của Hypebol


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
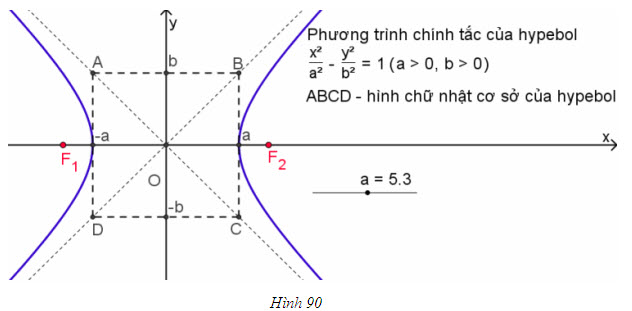
Tọa độ các tiêu điểm của hypebol phụ thuộc vào dạng chính tắc của hypebol. Nếu hypebol có dạng chính tắc x²/a² - y²/b² = 1 hoặc -x²/a² + y²/b² = 1, thì tọa độ tiêu điểm sẽ được xác định như sau.
Xác định tọa độ tiêu điểm của Hypebol
Hypebol dạng x²/a² - y²/b² = 1
Với hypebol có dạng x²/a² - y²/b² = 1, các tiêu điểm có tọa độ là F1(-c; 0) và F2(c; 0), trong đó c = √(a² + b²).Hypebol dạng -x²/a² + y²/b² = 1
Đối với hypebol dạng -x²/a² + y²/b² = 1, các tiêu điểm có tọa độ là F1(0; -c) và F2(0; c), với c = √(a² + b²).Ví dụ minh họa:
Giả sử ta có hypebol x²/9 - y²/16 = 1. Trong trường hợp này, a² = 9, b² = 16, vậy a = 3 và b = 4. Ta tính được c = √(9 + 16) = √25 = 5. Do đó, tọa độ các tiêu điểm là F1(-5; 0) và F2(5; 0). Từ những thông tin trên, ta có thể dễ dàng xác định được tọa độ các tiêu điểm của hypebol bất kỳ dựa trên dạng chính tắc của nó. Việc hiểu rõ công thức và áp dụng đúng dạng chính tắc là chìa khóa để giải quyết bài toán này chính xác. Hãy nhớ rằng, 'c' luôn luôn lớn hơn 'a' và 'b'.Sản phẩm liên quan: thừa số chung là gì
Xem thêm: hình xăm hổ lên núi
Xem thêm: con bọ cánh cam tiếng anh là gì
Xem thêm: 1 cây sắt phi 16 dài bao nhiêu mét
Sản phẩm hữu ích: liếc dao của đức