Tích Phân Bội Ba

Mô tả sản phẩm

Tích phân bội ba là một khái niệm quan trọng trong giải tích đa biến, cho phép tính toán thể tích của một khối trong không gian ba chiều hoặc tính toán tích phân của một hàm trên một miền ba chiều. Nó mở rộng khái niệm tích phân kép lên không gian ba chiều và có nhiều ứng dụng quan trọng trong vật lý, kỹ thuật và các lĩnh vực khác.

Khái niệm Tích Phân Bội Ba

Định nghĩa và ký hiệu

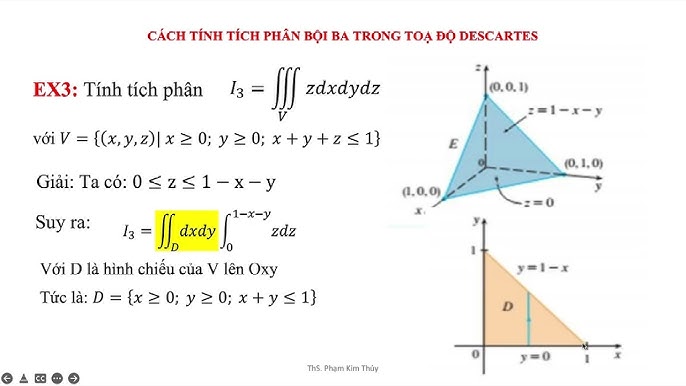
Tích phân bội ba của một hàm f(x, y, z) trên một miền V trong không gian ba chiều được định nghĩa như sau: ∫∫∫_V f(x, y, z) dV = ∫∫∫_V f(x, y, z) dx dy dz Trong đó: * f(x, y, z) là hàm số liên tục trên miền V. * dV là phần tử thể tích, thường được biểu diễn bằng dx dy dz (theo thứ tự tích phân). Thứ tự này có thể thay đổi tùy thuộc vào miền tích phân và phương pháp tính toán. * V là miền tích phân trong không gian ba chiều. Miền V thường được định nghĩa bằng các bất phương trình liên quan đến x, y, và z. Việc xác định đúng miền tích phân là bước quan trọng để tính toán tích phân bội ba.

Các bước tính toán tích phân bội ba

Tính toán tích phân bội ba thường được thực hiện bằng cách chuyển đổi tích phân bội ba thành tích phân lặp. Quá trình này bao gồm: 1. **Xác định miền tích phân V:** Mô tả miền V bằng các bất phương trình liên quan đến x, y và z. 2. **Chọn thứ tự tích phân:** Chọn thứ tự tích phân dx, dy, dz. Việc lựa chọn này phụ thuộc vào hình dạng của miền V và có thể ảnh hưởng đến độ phức tạp của phép tính. Thông thường, ta lựa chọn thứ tự tích phân sao cho việc tính toán các tích phân từng phần được đơn giản nhất. 3. **Thiết lập các cận tích phân:** Dựa trên miền V, xác định cận tích phân cho mỗi biến. 4. **Tính toán tích phân lặp:** Tính toán tích phân từng phần, bắt đầu từ tích phân bên trong nhất và tiến ra ngoài.

Ví dụ minh họa

Hãy tính tích phân bội ba của hàm f(x, y, z) = x + y + z trên khối lập phương V được xác định bởi 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1. ∫∫∫_V (x + y + z) dV = ∫₀¹ ∫₀¹ ∫₀¹ (x + y + z) dx dy dz Chúng ta sẽ tính tích phân lặp như sau: ∫₀¹ ∫₀¹ [(x²/2 + xy + xz) |_x=0^x=1] dy dz = ∫₀¹ ∫₀¹ (1/2 + y + z) dy dz Tiếp tục tính tích phân: ∫₀¹ [(y/2 + y²/2 + yz) |_y=0^y=1] dz = ∫₀¹ (1 + z) dz Cuối cùng: [(z + z²/2) |_z=0^z=1] = 3/2 Vậy tích phân bội ba của f(x, y, z) = x + y + z trên khối lập phương V là 3/2.

Ứng dụng của Tích Phân Bội Ba

Tích phân bội ba có rất nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:

Tính toán thể tích

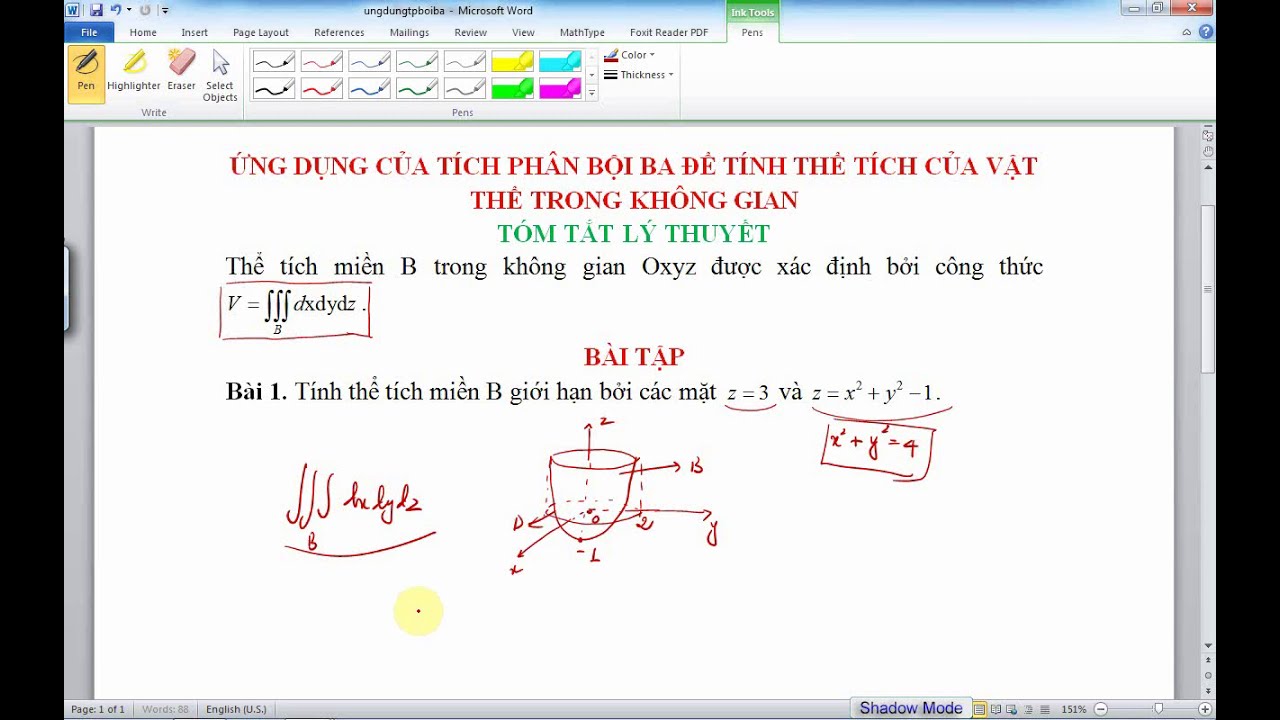
Đây là một trong những ứng dụng quan trọng nhất của tích phân bội ba. Bằng cách tính tích phân bội ba của hàm f(x, y, z) = 1 trên một miền V, ta có thể tính được thể tích của miền V.

Tính toán khối lượng

Nếu biết mật độ của một vật thể tại mỗi điểm trong không gian, ta có thể sử dụng tích phân bội ba để tính toán khối lượng của vật thể đó.

Tính toán trọng tâm

Tích phân bội ba giúp ta xác định trọng tâm của một vật thể có hình dạng phức tạp.

Trong vật lý và kỹ thuật

Tích phân bội ba được sử dụng rộng rãi trong nhiều lĩnh vực của vật lý và kỹ thuật, chẳng hạn như tính toán điện trường, từ trường, lực hấp dẫn, dòng chảy chất lỏng, và nhiều ứng dụng khác.

Tích phân bội ba và hệ tọa độ khác

Ngoài hệ tọa độ Descartes, tích phân bội ba cũng có thể được tính toán trong các hệ tọa độ khác như hệ tọa độ trụ và hệ tọa độ cầu. Việc lựa chọn hệ tọa độ phù hợp sẽ giúp đơn giản hóa quá trình tính toán, đặc biệt khi miền tích phân có hình dạng đối xứng.

Hệ tọa độ trụ

Trong hệ tọa độ trụ, ta thay đổi biến số từ (x, y, z) thành (ρ, θ, z), với ρ là khoảng cách từ điểm đến trục z, θ là góc giữa trục x và hình chiếu của điểm lên mặt phẳng xy, và z là tọa độ z. Phần tử thể tích trong hệ tọa độ trụ là ρ dρ dθ dz.

Hệ tọa độ cầu

Trong hệ tọa độ cầu, ta thay đổi biến số từ (x, y, z) thành (ρ, θ, φ), với ρ là khoảng cách từ điểm đến gốc tọa độ, θ là góc giữa trục x và hình chiếu của điểm lên mặt phẳng xy, và φ là góc giữa trục z và đoạn thẳng nối điểm với gốc tọa độ. Phần tử thể tích trong hệ tọa độ cầu là ρ² sinφ dρ dθ dφ. Việc hiểu và thành thạo tích phân bội ba là một kỹ năng quan trọng đối với sinh viên và các nhà nghiên cứu trong nhiều lĩnh vực. Hi vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về khái niệm, phương pháp tính toán và các ứng dụng của tích phân bội ba.

Xem thêm: tích kiệm hay tiết kiệm

Sản phẩm hữu ích: thi vị hóa là gì

Sản phẩm liên quan: sủi ma tiếng thái