Tập Nghiệm Bất Phương Trình
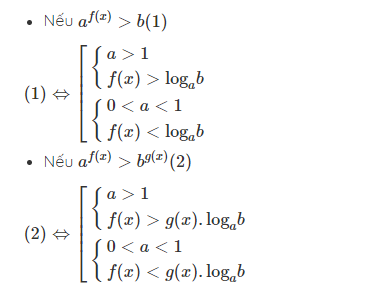


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tập nghiệm của bất phương trình phụ thuộc hoàn toàn vào dạng của bất phương trình đó. Không có một câu trả lời chung nào cho tất cả các bất phương trình. Để tìm tập nghiệm, bạn cần giải bất phương trình cụ thể. Hãy cùng tìm hiểu cách xác định tập nghiệm của các loại bất phương trình khác nhau.
Các Loại Bất Phương Trình và Cách Xác Định Tập Nghiệm
Bất Phương Trình Bậc Nhất Một Ẩn
Bất phương trình bậc nhất một ẩn có dạng ax + b > 0, ax + b < 0, ax + b ≥ 0 hoặc ax + b ≤ 0, với a và b là các số thực, a ≠ 0. Để giải, ta thực hiện các phép biến đổi tương đương để đưa về dạng x > c, x < c, x ≥ c hoặc x ≤ c, trong đó c là một số thực. Tập nghiệm sẽ là khoảng, đoạn hoặc nửa khoảng tương ứng. Ví dụ: Giải bất phương trình 2x + 3 > 7. Ta có: 2x > 4 => x > 2. Tập nghiệm là (2; +∞).Bất Phương Trình Bậc Hai Một Ẩn
Bất phương trình bậc hai một ẩn có dạng ax² + bx + c > 0, ax² + bx + c < 0, ax² + bx + c ≥ 0 hoặc ax² + bx + c ≤ 0, với a, b, c là các số thực, a ≠ 0. Để giải, ta cần tìm nghiệm của phương trình ax² + bx + c = 0. Dựa vào dấu của a và nghiệm của phương trình, ta xác định được tập nghiệm. Ví dụ: Giải bất phương trình x² - 4x + 3 < 0. Phương trình x² - 4x + 3 = 0 có hai nghiệm x = 1 và x = 3. Do a = 1 > 0, nên tập nghiệm là (1; 3).Hệ Bất Phương Trình
Hệ bất phương trình là một hệ gồm nhiều bất phương trình. Tập nghiệm của hệ bất phương trình là giao của các tập nghiệm của từng bất phương trình trong hệ.Bất Phương Trình Mũ và Logarit
Bất phương trình mũ và logarit được giải bằng cách sử dụng tính chất của hàm mũ và hàm logarit. Việc giải quyết các bất phương trình này thường đòi hỏi kiến thức về hàm số và tính chất của chúng. Để tìm tập nghiệm chính xác của bất phương trình cụ thể, bạn cần áp dụng các kỹ thuật giải thích hợp dựa trên loại bất phương trình. Hãy nhớ rằng việc hiểu rõ các quy tắc và tính chất đại số là vô cùng quan trọng trong việc giải bất phương trình.Xem thêm: cách chế biến ốc vòi voi
Sản phẩm liên quan: vẽ đường tròn trong cad
Xem thêm: thế năng đàn hồi của vật là
Xem thêm: toan nang cao lop 2