Sigma trong Toán học
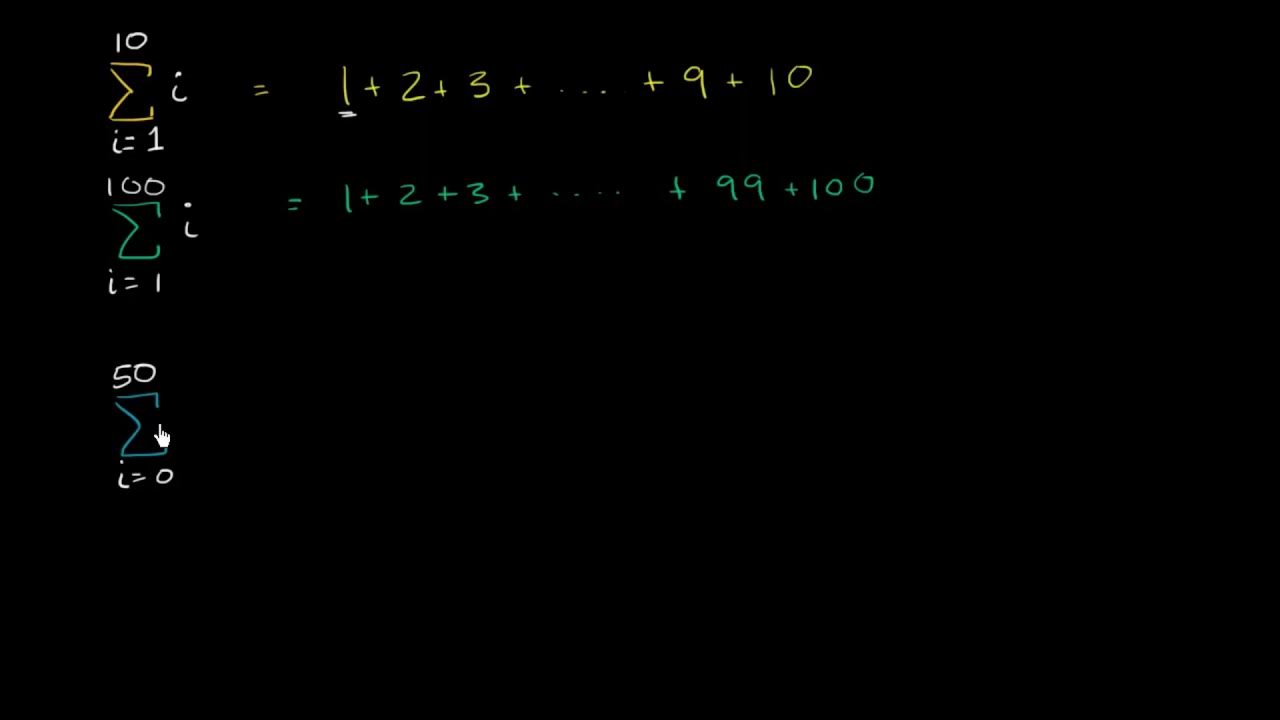

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Sigma (Σ) trong toán học là ký hiệu dùng để biểu diễn phép tổng. Nó cho phép viết gọn một chuỗi các số hạng cần cộng lại với nhau, giúp cho việc biểu diễn toán học trở nên ngắn gọn và dễ hiểu hơn. Bài viết này sẽ giải thích chi tiết về ký hiệu sigma, cách sử dụng và các ví dụ minh họa.
Tổng Quát về Ký Hiệu Sigma
Cấu trúc của Sigma
Ký hiệu sigma có cấu trúc tổng quát như sau: ∑i=mn ai. Trong đó: * Σ: ký hiệu sigma (uppercase của chữ cái Hy Lạp sigma). * i: chỉ số của phép tổng (biến đếm). * m: giá trị bắt đầu của chỉ số i (giới hạn dưới). * n: giá trị kết thúc của chỉ số i (giới hạn trên). * ai: biểu thức tổng quát của số hạng thứ i. Ví dụ: ∑i=15 i có nghĩa là tổng các số từ 1 đến 5: 1 + 2 + 3 + 4 + 5 = 15. Ở đây, i là biến đếm, m = 1, n = 5, và ai = i.Các Ví dụ về Sử dụng Sigma
Dưới đây là một số ví dụ minh họa cách sử dụng ký hiệu sigma trong các bài toán khác nhau: * ∑k=03 (2k + 1) = (2(0) + 1) + (2(1) + 1) + (2(2) + 1) + (2(3) + 1) = 1 + 3 + 5 + 7 = 16. * ∑j=14 j² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30. * ∑n=1∞ (1/2)n là một tổng vô hạn, biểu diễn chuỗi hình học.Ứng dụng của Sigma trong Toán Học
Ký hiệu sigma được sử dụng rộng rãi trong nhiều lĩnh vực toán học, bao gồm:Tính Toán Chuỗi Số
Sigma là công cụ quan trọng để tính toán tổng của các chuỗi số, cả chuỗi hữu hạn và chuỗi vô hạn. Việc sử dụng sigma giúp biểu diễn các chuỗi số một cách gọn gàng và dễ dàng thao tác.Tính Toán Tích Phân
Trong giải tích, sigma được sử dụng như một khái niệm nền tảng để định nghĩa tích phân. Tích phân có thể được hiểu như là một giới hạn của tổng Riemann, sử dụng ký hiệu sigma để biểu diễn.Thống kê và Xác suất
Sigma được dùng trong thống kê và xác suất để biểu diễn kỳ vọng, phương sai và các đại lượng thống kê khác.Xem thêm: bầu ăn tiết canh dê được không
Sản phẩm liên quan: ion hóa là gì
Xem thêm: oxit nào là oxit lưỡng tính
Xem thêm: nêu các biện pháp tiết kiệm điện năng lớp 8
Xem thêm: tổng 3 góc của 1 tam giác vuông