Quy tắc hình bình hành vecto

Mô tả sản phẩm

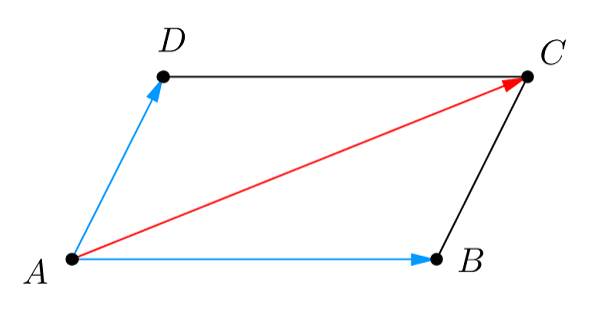
Quy tắc hình bình hành vecto phát biểu rằng: tổng của hai vecto $\vec{a}$ và $\vec{b}$ là một vecto $\vec{c}$ được xác định bằng đường chéo của hình bình hành tạo bởi hai vecto đó. Nói cách khác, để tìm tổng của hai vecto, ta vẽ hai vecto đó cùng gốc, rồi dựng hình bình hành. Vecto tổng sẽ là đường chéo xuất phát từ gốc chung đó.

Chứng minh quy tắc hình bình hành vecto

Phương pháp tọa độ

Giả sử vecto $\vec{a} = (x_a, y_a)$ và vecto $\vec{b} = (x_b, y_b)$. Theo quy tắc cộng vecto, ta có: $\vec{c} = \vec{a} + \vec{b} = (x_a + x_b, y_a + y_b)$. Điều này tương ứng với tọa độ đỉnh của hình bình hành, chứng minh quy tắc hình bình hành.

Phương pháp hình học

Xét hình bình hành ABCD với $\vec{AB} = \vec{a}$ và $\vec{AD} = \vec{b}$. Theo định nghĩa phép cộng vecto, ta có $\vec{AB} + \vec{AD} = \vec{AC}$. Do ABCD là hình bình hành nên $\vec{AC}$ là đường chéo của hình bình hành, điều này chứng minh quy tắc hình bình hành.

Ứng dụng của quy tắc hình bình hành vecto

Quy tắc hình bình hành vecto có nhiều ứng dụng quan trọng trong vật lý và kỹ thuật, ví dụ như:

• Phân tích lực:
• Tính toán chuyển động của vật thể:
• Giải các bài toán liên quan đến cân bằng lực:

Hiểu rõ quy tắc hình bình hành vecto là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong lĩnh vực toán học và vật lý.

Sản phẩm hữu ích: nitơ có nguyên tử khối là bảo nhiều

Sản phẩm hữu ích: máy phát điện xoay chiều hoạt động

Xem thêm: nêu tính chất hóa học của rượu etylic