Quy Luật Dãy Số: Tìm Hiểu Và Áp Dụng


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Quy luật dãy số là một khái niệm toán học dùng để mô tả mối quan hệ giữa các số trong một dãy, giúp dự đoán số hạng tiếp theo hoặc tìm ra công thức tổng quát. Có nhiều loại quy luật dãy số khác nhau, từ đơn giản đến phức tạp. Việc hiểu và áp dụng quy luật dãy số rất quan trọng trong nhiều lĩnh vực, từ giải toán đến lập trình và nghiên cứu khoa học.
Các Loại Quy Luật Dãy Số Thường Gặp
Dãy Số Cộng
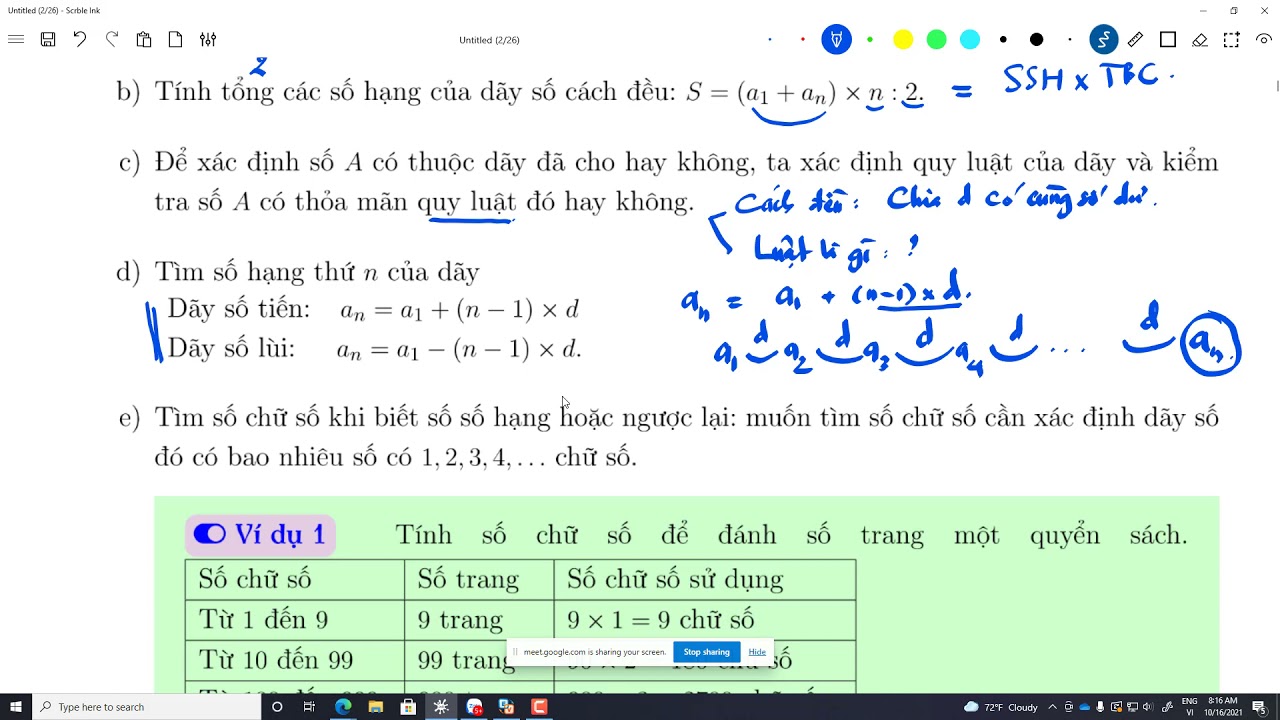
Đây là loại dãy số mà hiệu giữa hai số hạng liên tiếp là một hằng số (gọi là công sai). Ví dụ: 1, 4, 7, 10, 13... (công sai là 3). Công thức tổng quát của dãy số cộng là: an = a1 + (n-1)d, trong đó an là số hạng thứ n, a1 là số hạng đầu tiên, và d là công sai.
Dãy Số Nhân
Trong dãy số nhân, thương giữa hai số hạng liên tiếp là một hằng số (gọi là công bội). Ví dụ: 2, 6, 18, 54... (công bội là 3). Công thức tổng quát của dãy số nhân là: an = a1 * r(n-1), trong đó an là số hạng thứ n, a1 là số hạng đầu tiên, và r là công bội.
Dãy Số Fibonacci
Dãy số Fibonacci là một dãy số mà mỗi số hạng (kể từ số hạng thứ ba) bằng tổng của hai số hạng trước đó. Ví dụ: 1, 1, 2, 3, 5, 8, 13... Dãy số này có nhiều ứng dụng trong tự nhiên và toán học.
Dãy Số Vuông
Dãy số này bao gồm các số chính phương, tức là bình phương của các số tự nhiên. Ví dụ: 1, 4, 9, 16, 25...
Dãy Số Lập Phương
Dãy số này bao gồm các số lập phương, tức là lập phương của các số tự nhiên. Ví dụ: 1, 8, 27, 64, 125...
Cách Xác Định Quy Luật Dãy Số
Để xác định quy luật của một dãy số, ta cần quan sát sự khác biệt giữa các số hạng liên tiếp. Nếu sự khác biệt là một hằng số, đó là dãy số cộng. Nếu thương giữa các số hạng liên tiếp là một hằng số, đó là dãy số nhân. Nếu không phải là dãy số cộng hay nhân, ta cần tìm kiếm các quy luật khác, ví dụ như dãy số Fibonacci, dãy số chính phương, hoặc các quy luật phức tạp hơn. Thường thì cần phải phân tích kỹ lưỡng và có thể cần đến kiến thức toán học cao hơn để tìm ra quy luật của một dãy số phức tạp.
Ứng Dụng Của Quy Luật Dãy Số
Quy luật dãy số được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm: giải các bài toán về dãy số, dự đoán xu hướng trong thống kê, lập trình máy tính (ví dụ: tạo các chuỗi số, mô hình hóa dữ liệu), mô tả các hiện tượng tự nhiên (ví dụ: dãy số Fibonacci xuất hiện trong cấu trúc xoắn ốc của vỏ ốc sên), và nhiều lĩnh vực khác nữa.
Sản phẩm liên quan: 100 bài đồng dao
Sản phẩm hữu ích: trạng ngữ la gì lớp 4
Xem thêm: bi quan có nghĩa là gì
Xem thêm: vế câu là gì lớp 5
Xem thêm: lớp 10 cần bao nhiêu quyển vở