Phương trình tiếp tuyến của đường tròn

Mô tả sản phẩm

Phương trình tiếp tuyến của đường tròn là công thức toán học giúp xác định đường thẳng tiếp xúc với đường tròn tại một điểm cụ thể. Việc tìm phương trình này phụ thuộc vào thông tin đã biết, ví dụ như tọa độ tâm, bán kính và điểm tiếp xúc hoặc chỉ có tọa độ tâm, bán kính và một điểm nằm trên tiếp tuyến.

Các trường hợp tìm phương trình tiếp tuyến

Trường hợp 1: Biết tọa độ tâm, bán kính và điểm tiếp xúc

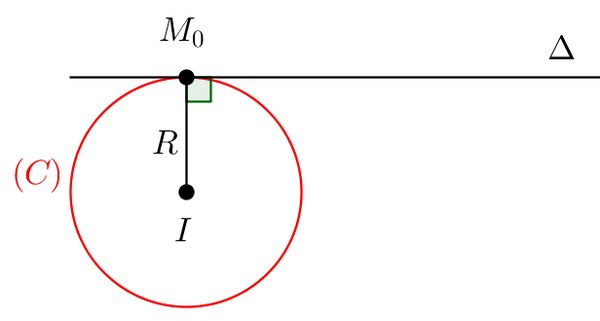
Giả sử đường tròn có tâm I(a; b) và bán kính R. Điểm tiếp xúc là M(x₀; y₀). Vectơ IM sẽ vuông góc với tiếp tuyến tại M. Phương trình tiếp tuyến được xác định bởi công thức: (x₀ - a)(x - a) + (y₀ - b)(y - b) = R².

Trường hợp 2: Biết tọa độ tâm, bán kính và một điểm nằm trên tiếp tuyến

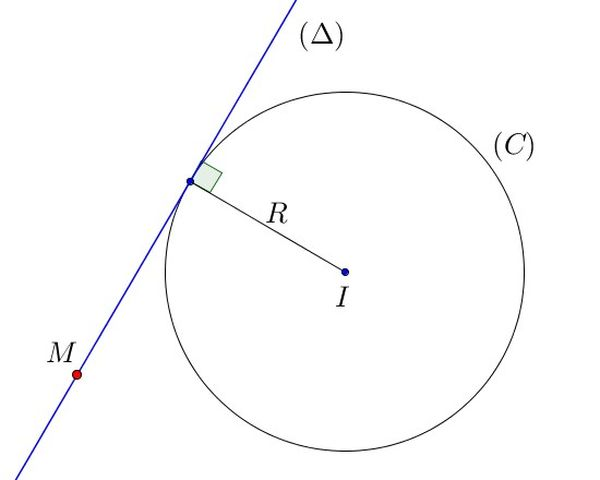
Trong trường hợp này, giả sử ta biết tâm I(a; b), bán kính R và một điểm A(x₁; y₁) nằm trên tiếp tuyến. Ta cần tìm hai tiếp tuyến đi qua điểm A. Phương trình đường thẳng đi qua A và có hệ số góc k là: y - y₁ = k(x - x₁). Khoảng cách từ tâm I đến đường thẳng này phải bằng bán kính R. Từ đó ta lập phương trình bậc hai để tìm k, sau đó thay k vào phương trình đường thẳng để tìm được phương trình tiếp tuyến.

Trường hợp 3: Biết phương trình đường tròn và một điểm nằm trên đường tròn

Nếu bạn biết phương trình đường tròn (x-a)² + (y-b)² = R² và một điểm M(x₀, y₀) nằm trên đường tròn, thì phương trình tiếp tuyến tại M là: (x₀-a)(x-a) + (y₀-b)(y-b) = R². Tóm lại, việc tìm phương trình tiếp tuyến của đường tròn phụ thuộc vào thông tin đã cho. Hiểu rõ các trường hợp khác nhau sẽ giúp bạn giải quyết các bài toán liên quan một cách hiệu quả. Hãy luyện tập nhiều bài tập để nắm vững kiến thức này.

Sản phẩm hữu ích: chứng minh công thức logarit

Sản phẩm hữu ích: nằm mơ trâu đuổi đánh con gì

Xem thêm: vật rơi tự do truyện

Sản phẩm liên quan: công thức tính đáy lớn đáy bé của hình thang