Chứng minh công thức logarit
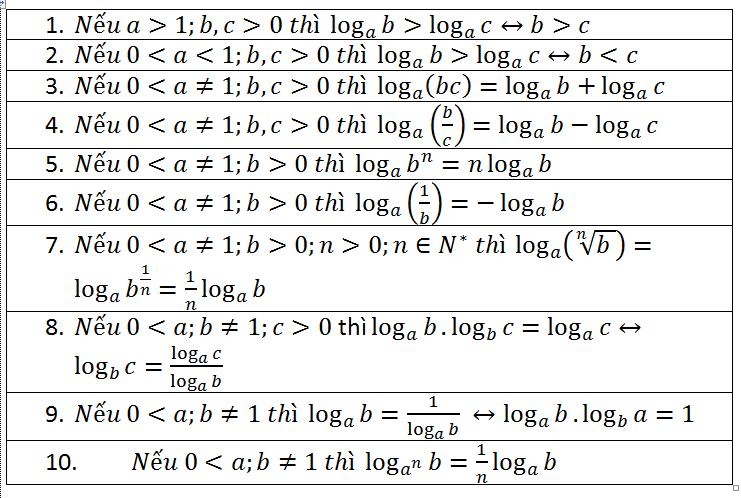
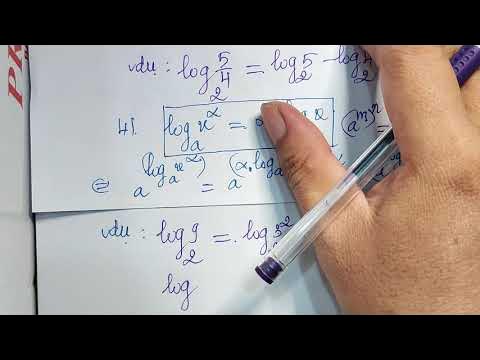
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Chứng minh công thức logarit là một quá trình toán học giúp hiểu rõ nguồn gốc và tính chất của các công thức logarit quan trọng. Bài viết này sẽ trình bày chi tiết cách chứng minh các công thức logarit cơ bản, giúp bạn nắm vững kiến thức và áp dụng vào giải toán hiệu quả.
Công thức logarit cơ bản và chứng minh
Logarit của tích
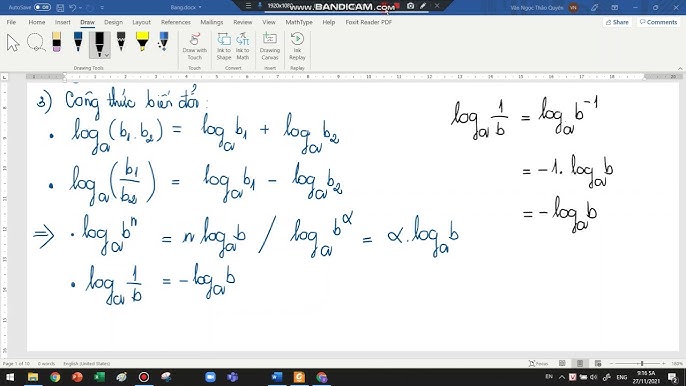
Công thức: loga(xy) = logax + logay (với a > 0, a ≠ 1, x > 0, y > 0) Chứng minh: Gọi m = logax và n = logay. Theo định nghĩa logarit, ta có am = x và an = y. Nhân hai đẳng thức này lại, ta được: am * an = x * y am+n = xy Theo định nghĩa logarit, ta suy ra loga(xy) = m + n = logax + logay. Vậy công thức được chứng minh.Logarit của thương
Công thức: loga(x/y) = logax - logay (với a > 0, a ≠ 1, x > 0, y > 0) Chứng minh: Tương tự như trên, gọi m = logax và n = logay. Ta có am = x và an = y. Chia hai đẳng thức này, ta được: am / an = x / y am-n = x/y Theo định nghĩa logarit, ta suy ra loga(x/y) = m - n = logax - logay. Vậy công thức được chứng minh.Logarit của lũy thừa
Công thức: loga(xp) = p * logax (với a > 0, a ≠ 1, x > 0) Chứng minh: Gọi m = logax. Theo định nghĩa logarit, ta có am = x. Lũy thừa cả hai vế lên p, ta được: (am)p = xp amp = xp Theo định nghĩa logarit, ta suy ra loga(xp) = mp = p * logax. Vậy công thức được chứng minh. Các công thức trên là nền tảng cho việc giải quyết nhiều bài toán logarit phức tạp hơn. Hiểu rõ cách chứng minh sẽ giúp bạn vận dụng linh hoạt và chính xác các công thức này.Sản phẩm liên quan: nhị thập là số mấy
Sản phẩm liên quan: tam giác abc vuông tại a
Sản phẩm hữu ích: hợp âm ngày chưa giông bão
Sản phẩm hữu ích: tính chất đường trung bình
Sản phẩm liên quan: cách tính giới hạn