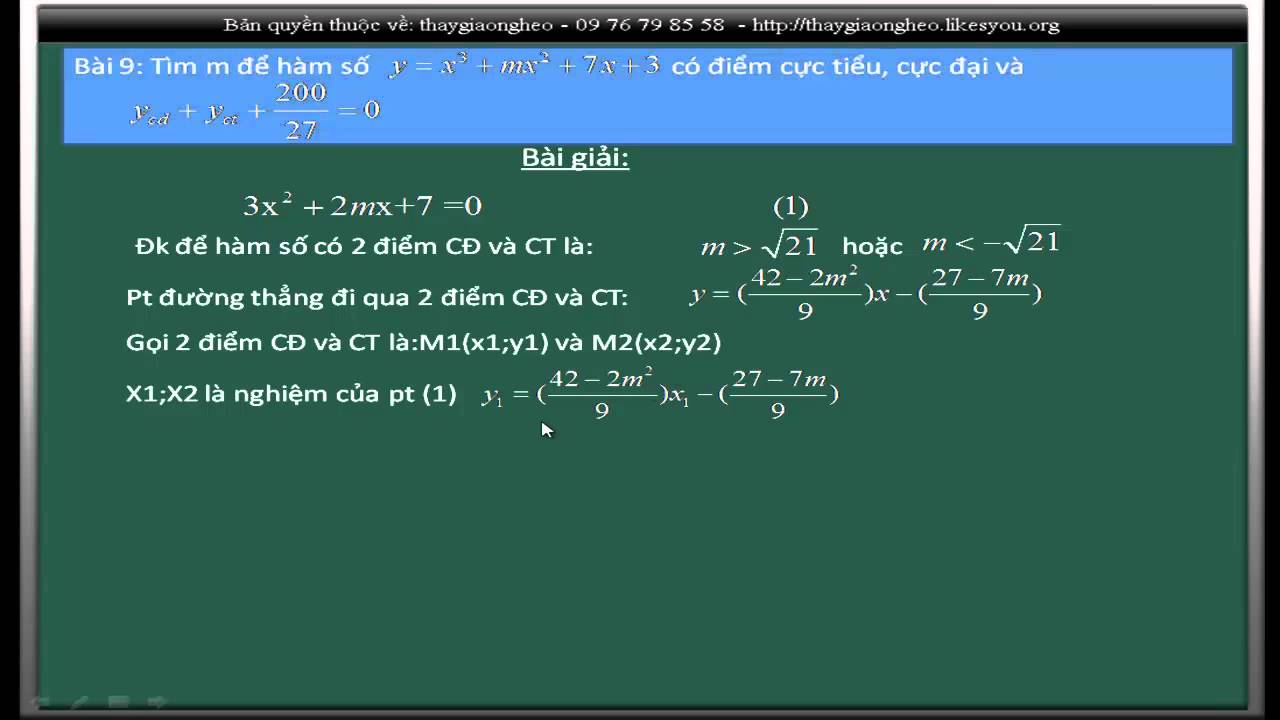
Phương trình đường thẳng đi qua 2 điểm cực trị của hàm số

Mô tả sản phẩm

Phương trình đường thẳng đi qua hai điểm cực trị của hàm số y = f(x) được xác định bằng cách tìm tọa độ của hai điểm cực trị, sau đó sử dụng công thức phương trình đường thẳng đi qua hai điểm.

Cách tìm phương trình đường thẳng đi qua 2 điểm cực trị

Bước 1: Tìm tọa độ điểm cực trị

Để tìm tọa độ điểm cực trị, ta cần tính đạo hàm của hàm số f'(x) và giải phương trình f'(x) = 0. Các nghiệm của phương trình này chính là hoành độ của các điểm cực trị. Thay các hoành độ này vào hàm số f(x) để tìm tung độ tương ứng.

Bước 2: Viết phương trình đường thẳng

Giả sử ta tìm được hai điểm cực trị là A(x1, y1) và B(x2, y2). Phương trình đường thẳng đi qua hai điểm A và B có dạng:
$\frac{y - y1}{x - x1} = \frac{y2 - y1}{x2 - x1}$
Hoặc có thể sử dụng công thức tổng quát:
y = ax + b
với a và b được tìm bằng cách giải hệ phương trình:
y1 = ax1 + b
y2 = ax2 + b

Trường hợp đặc biệt: Hàm số bậc ba

Đối với hàm số bậc ba y = ax³ + bx² + cx + d (a ≠ 0), phương trình đường thẳng đi qua hai điểm cực trị có dạng đơn giản hơn:
y = -$\frac{b}{3a}$x + d - $\frac{bc}{9a}$
Công thức này giúp ta tính toán nhanh chóng hơn mà không cần tìm tọa độ cụ thể của các điểm cực trị. Việc sử dụng công thức này giúp tiết kiệm thời gian và giảm thiểu rủi ro sai sót trong tính toán. Lưu ý: Phương pháp này chỉ áp dụng cho các hàm số có hai điểm cực trị. Đối với các hàm số không có điểm cực trị hoặc có nhiều hơn hai điểm cực trị, cần sử dụng các phương pháp khác để tìm đường thẳng phù hợp.

Sản phẩm hữu ích: biên nhiệt độ là gì

Sản phẩm hữu ích: vai trò của nước đối với môi trường

Xem thêm: quy tắc lũy thừa

Xem thêm: vở lớp 6 gồm những gì 2023

Sản phẩm liên quan: từ trái nghĩa với đoàn kết