Phương trình tiếp tuyến của đường tròn

Mô tả sản phẩm

Phương trình tiếp tuyến của đường tròn là một công thức toán học giúp xác định phương trình của đường thẳng tiếp xúc với đường tròn tại một điểm cụ thể. Việc tìm phương trình tiếp tuyến phụ thuộc vào thông tin đã biết, có thể là tọa độ tiếp điểm và phương trình đường tròn, hoặc tọa độ điểm nằm ngoài đường tròn và phương trình đường tròn.

Các trường hợp tìm phương trình tiếp tuyến

Trường hợp 1: Biết tọa độ tiếp điểm và phương trình đường tròn

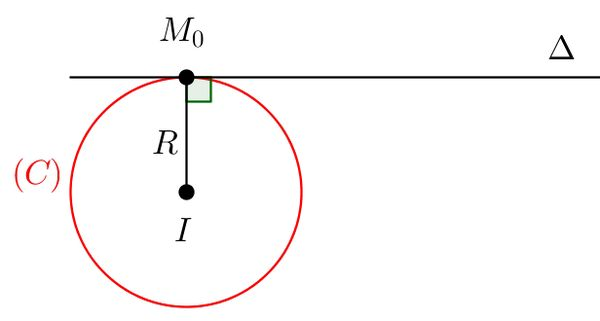
Giả sử đường tròn có phương trình (x - a)² + (y - b)² = r², với tâm I(a, b) và bán kính r. Tiếp điểm là M(x₀, y₀). Vecto IM vuông góc với tiếp tuyến tại M. Phương trình tiếp tuyến có dạng: (x₀ - a)(x - a) + (y₀ - b)(y - b) = r².

Trường hợp 2: Biết điểm nằm ngoài đường tròn và phương trình đường tròn

Giả sử điểm nằm ngoài đường tròn là A(x₁, y₁) và phương trình đường tròn là (x - a)² + (y - b)² = r². Có hai tiếp tuyến đi qua A. Gọi M(x, y) là tiếp điểm. Ta có phương trình: (x - a)² + (y - b)² = r² và phương trình đường thẳng AM có hệ số góc k: (y - y₁) = k(x - x₁). Thay y từ phương trình đường thẳng AM vào phương trình đường tròn, ta giải phương trình bậc hai theo x. Điều kiện để có nghiệm là phương trình bậc hai có nghiệm kép (delta = 0). Từ đó tìm được k, và phương trình tiếp tuyến.

Trường hợp 3: Phương trình tiếp tuyến song song hoặc vuông góc với một đường thẳng cho trước

Nếu tiếp tuyến song song với đường thẳng y = mx + c, thì hệ số góc của tiếp tuyến là m. Nếu tiếp tuyến vuông góc với đường thẳng y = mx + c, thì hệ số góc của tiếp tuyến là -1/m (với m≠0). Từ đó ta có thể thiết lập phương trình tiếp tuyến. Tóm lại, việc tìm phương trình tiếp tuyến của đường tròn phụ thuộc vào thông tin đã biết. Hiểu rõ các trường hợp và áp dụng công thức phù hợp sẽ giúp bạn giải quyết bài toán một cách chính xác. Bài viết này đã cung cấp những kiến thức cơ bản và các ví dụ để bạn có thể dễ dàng hiểu và áp dụng.

Sản phẩm liên quan: ôn tập tính chất cơ bản của lớp 5

Sản phẩm hữu ích: cơ quan tương tự là những cơ quan

Sản phẩm hữu ích: đặc điểm của từ trường

Sản phẩm liên quan: phép tính lũy thừa