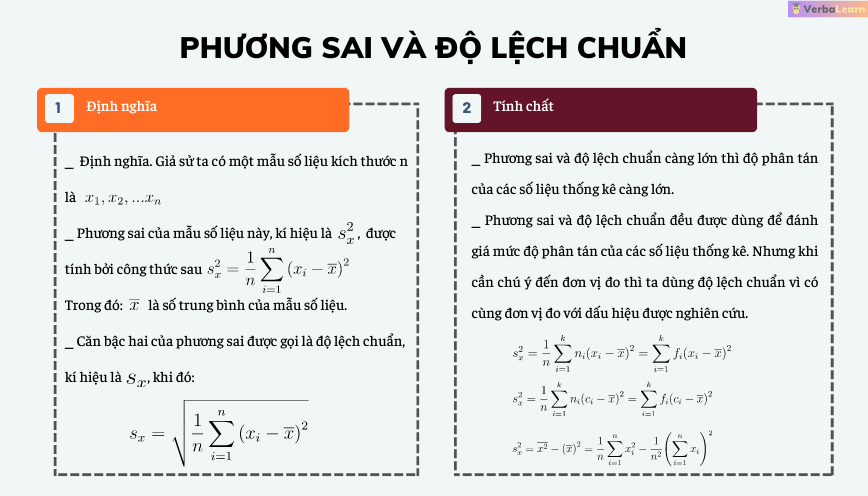
Phương Sai Mẫu và Phương Sai Mẫu Hiệu Chỉnh


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Phương sai mẫu là thước đo mức độ phân tán của dữ liệu trong một mẫu, trong khi phương sai mẫu hiệu chỉnh là một ước lượng không chệch của phương sai của quần thể. Phương sai mẫu thường được tính toán bằng cách chia tổng bình phương sai lệch cho số lượng quan sát (n), còn phương sai mẫu hiệu chỉnh thì chia cho n-1. Sự khác biệt này quan trọng vì phương sai mẫu hiệu chỉnh cung cấp một ước lượng chính xác hơn về phương sai của quần thể, đặc biệt là khi kích thước mẫu nhỏ.
Phương Sai Mẫu
Công thức và Cách Tính
Phương sai mẫu (ký hiệu là s²) được tính bằng công thức:
s² = Σ(xi - x̄)² / n
Trong đó:
• xi là giá trị quan sát thứ i.
• x̄ là trung bình mẫu.
• n là số lượng quan sát trong mẫu.
Ví dụ: Nếu bạn có mẫu dữ liệu {2, 4, 6, 8}, trung bình mẫu x̄ = 5. Phương sai mẫu sẽ là: s² = [(2-5)² + (4-5)² + (6-5)² + (8-5)²] / 4 = 5
Phương Sai Mẫu Hiệu Chỉnh
Công thức và Cách Tính
Phương sai mẫu hiệu chỉnh (ký hiệu là s²hiệu chỉnh) được tính bằng công thức:
s²hiệu chỉnh = Σ(xi - x̄)² / (n - 1)
Trong đó:
• xi là giá trị quan sát thứ i.
• x̄ là trung bình mẫu.
• n là số lượng quan sát trong mẫu.
Với cùng ví dụ trên, phương sai mẫu hiệu chỉnh sẽ là: s²hiệu chỉnh = [(2-5)² + (4-5)² + (6-5)² + (8-5)²] / (4 - 1) = 6.67
Tại sao cần sử dụng phương sai mẫu hiệu chỉnh?
Phương sai mẫu hiệu chỉnh là một ước lượng không chệch của phương sai quần thể. Điều này có nghĩa là, trong nhiều lần lấy mẫu, trung bình của các phương sai mẫu hiệu chỉnh sẽ xấp xỉ phương sai của quần thể. Phương sai mẫu thông thường lại là một ước lượng chệch, có xu hướng đánh giá thấp phương sai của quần thể, đặc biệt khi kích thước mẫu nhỏ. Vì vậy, phương sai mẫu hiệu chỉnh thường được ưu tiên sử dụng, nhất là khi n nhỏ, để có được ước lượng chính xác hơn về phương sai của quần thể.
Ứng dụng thực tiễn
Cả phương sai mẫu và phương sai mẫu hiệu chỉnh đều được sử dụng rộng rãi trong thống kê để đo lường sự phân tán của dữ liệu, phục vụ cho việc phân tích dữ liệu, kiểm định giả thuyết và xây dựng các mô hình thống kê. Việc lựa chọn giữa hai loại phương sai phụ thuộc vào mục đích nghiên cứu và kích thước mẫu.
Sản phẩm hữu ích: đề thi toán hk2 lớp 2
Sản phẩm hữu ích: nguyên tố cơ bản
Xem thêm: ví dụ như là
Sản phẩm liên quan: vioedu toán lớp 3 kì 1
Xem thêm: câu kiêm ngữ trong tiếng trung