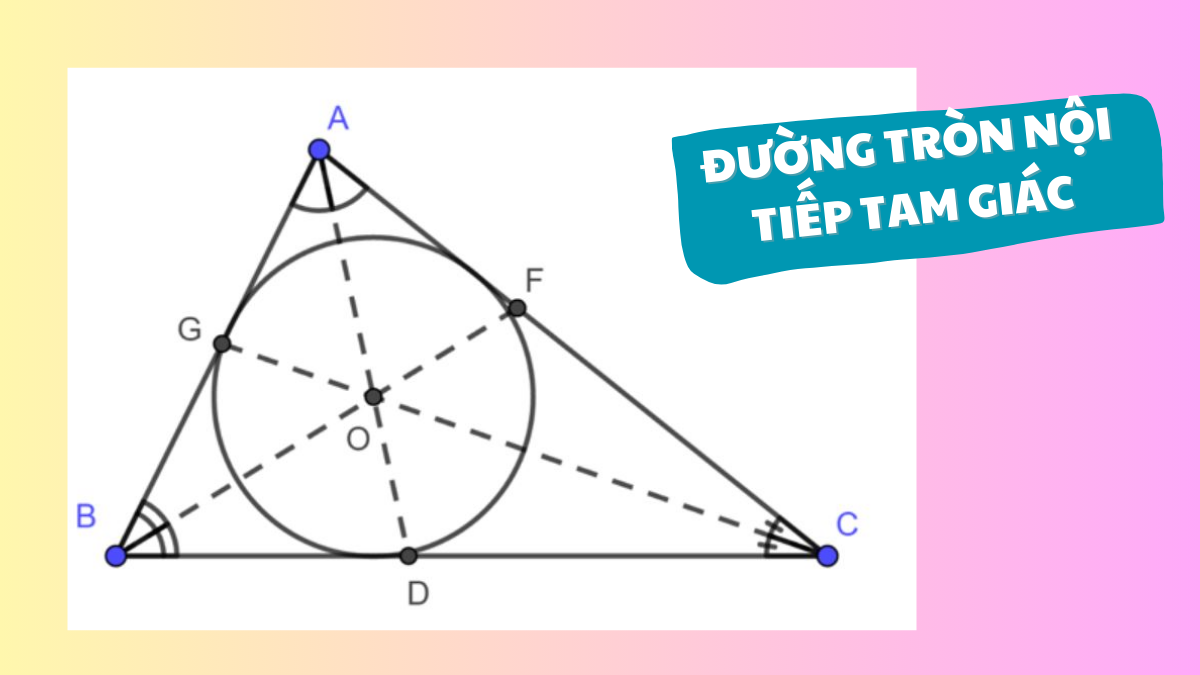
Nội Tiếp Đường Tròn Là Gì?

Mô tả sản phẩm

Nội tiếp đường tròn là khi một đa giác có tất cả các đỉnh nằm trên đường tròn. Nói cách khác, tất cả các đỉnh của đa giác đều nằm trên chu vi của đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp đa giác.

Các khái niệm liên quan

Đường tròn ngoại tiếp

Đường tròn ngoại tiếp là đường tròn đi qua tất cả các đỉnh của một đa giác. Không phải mọi đa giác đều có đường tròn ngoại tiếp. Ví dụ, một hình bình hành thông thường không có đường tròn ngoại tiếp, trừ khi nó là hình chữ nhật.

Đa giác nội tiếp

Một đa giác được gọi là đa giác nội tiếp nếu tất cả các đỉnh của nó nằm trên cùng một đường tròn. Tam giác luôn luôn là đa giác nội tiếp. Tuy nhiên, không phải tất cả các tứ giác đều là đa giác nội tiếp. Một tứ giác nội tiếp phải thỏa mãn một số điều kiện đặc biệt, chẳng hạn như tổng hai góc đối diện bằng 180 độ.

Ứng dụng của nội tiếp đường tròn

Hiểu về khái niệm nội tiếp đường tròn rất quan trọng trong nhiều lĩnh vực toán học, bao gồm hình học phẳng, hình học không gian và lượng giác. Nó được sử dụng để giải quyết các bài toán liên quan đến tính toán độ dài, góc, diện tích của các hình học phẳng. Ví dụ, công thức tính diện tích tam giác có thể được sử dụng khi biết bán kính đường tròn ngoại tiếp và các cạnh của tam giác. Trong hình học không gian, khái niệm nội tiếp được mở rộng để nghiên cứu các đa diện nội tiếp mặt cầu.

Ví dụ về đa giác nội tiếp

Một số ví dụ về đa giác nội tiếp bao gồm: tam giác, hình chữ nhật, hình vuông, các đa giác đều (tam giác đều, tứ giác đều, ngũ giác đều, v.v...). Lưu ý rằng không phải tất cả các tứ giác đều là nội tiếp. Một hình thang cân là một ví dụ về tứ giác nội tiếp.

Sản phẩm liên quan: tính chất của axit clohiđric

Sản phẩm hữu ích: thế nào là liên kết cộng hóa trị

Sản phẩm hữu ích: cá lóc bông cảnh