Lý thuyết Toán 9 Học kì 1


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Bạn đang tìm kiếm lý thuyết Toán 9 học kì 1 để ôn tập và chuẩn bị cho các bài kiểm tra? Bài viết này sẽ tổng hợp đầy đủ các kiến thức quan trọng của chương trình Toán lớp 9 học kì 1, giúp bạn nắm vững các định nghĩa, định lý và công thức cần thiết.
Chương 1: Căn bậc hai
1.1 Khái niệm căn bậc hai
Căn bậc hai của một số a không âm là một số x sao cho x² = a. Mỗi số a không âm có đúng hai căn bậc hai là √a và -√a. √a được gọi là căn bậc hai số học của a.
1.2 Tính chất của căn bậc hai
Bài học này trình bày các tính chất quan trọng của căn bậc hai, bao gồm tính chất liên hệ giữa căn bậc hai và lũy thừa, các phép toán với căn bậc hai (cộng, trừ, nhân, chia), và cách rút gọn biểu thức chứa căn bậc hai.
1.3 Biến đổi đơn giản biểu thức chứa căn bậc hai
Phần này hướng dẫn cách biến đổi các biểu thức chứa căn bậc hai về dạng đơn giản nhất, sử dụng các quy tắc và tính chất đã học ở phần trước.
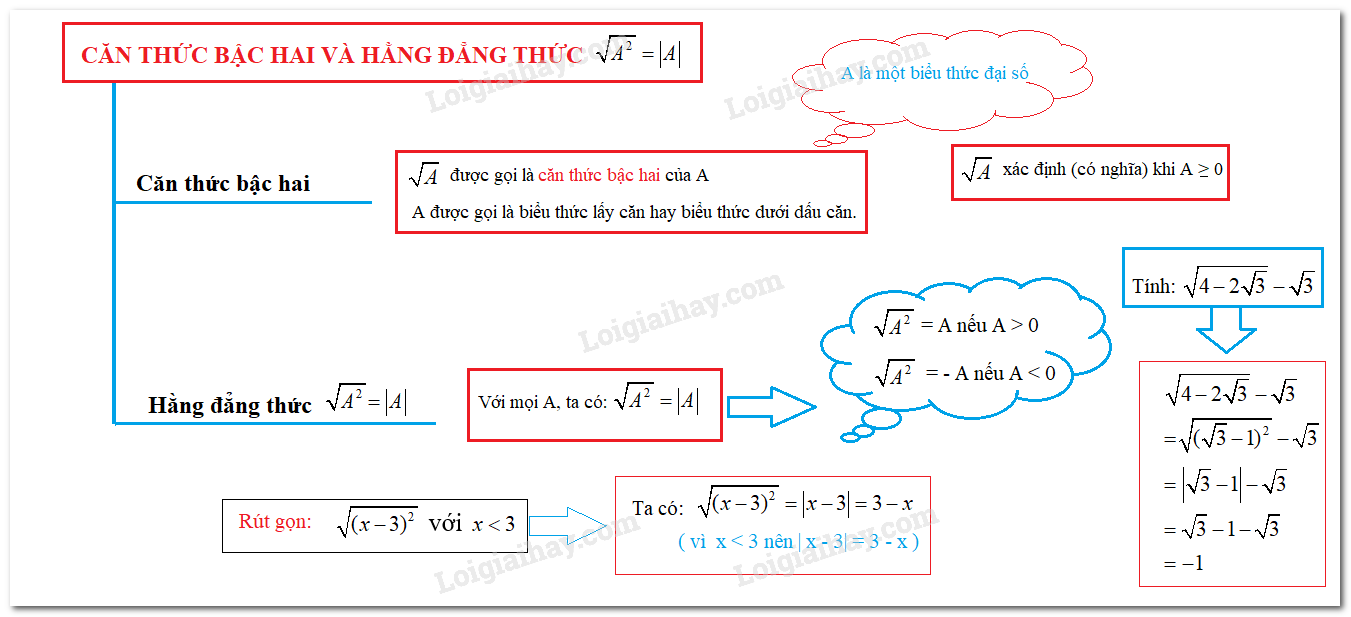
Chương 2: Căn thức bậc hai
2.1 Khái niệm căn thức bậc hai
Căn thức bậc hai là biểu thức có dạng √A, trong đó A là một biểu thức đại số. Bài học sẽ định nghĩa rõ ràng về căn thức bậc hai và các điều kiện để căn thức có nghĩa.
2.2 Hàm số y = √x
Phần này nghiên cứu hàm số căn bậc hai y = √x, bao gồm tập xác định, tính chất, đồ thị hàm số và ứng dụng của hàm số này.
2.3 Rút gọn biểu thức chứa căn thức bậc hai
Giải thích các phương pháp rút gọn biểu thức chứa căn thức bậc hai, bao gồm sử dụng các phép toán và các quy tắc biến đổi.
Chương 3: Hệ thức lượng trong tam giác vuông
3.1 Định lý Pitago
Định lý Pitago là một trong những định lý quan trọng nhất trong hình học, được sử dụng để tính độ dài các cạnh trong tam giác vuông.
3.2 Hệ thức lượng trong tam giác vuông
Phần này trình bày các hệ thức lượng trong tam giác vuông, bao gồm các công thức liên hệ giữa các cạnh và đường cao của tam giác vuông.
3.3 Ứng dụng hệ thức lượng trong tam giác vuông
Ứng dụng các hệ thức lượng trong tam giác vuông để giải các bài toán tính toán độ dài các cạnh, đường cao, diện tích tam giác vuông.
Sản phẩm liên quan: nghich ly ke sat nhan
Sản phẩm liên quan: mồi câu cá chép mùa đông
Xem thêm: một hình hộp chữ nhật có diện tích xung quanh
Xem thêm: cách chế biến ốc vòi voi
Sản phẩm hữu ích: tam mao tv sinh năm bao nhiêu