Lim của hằng số


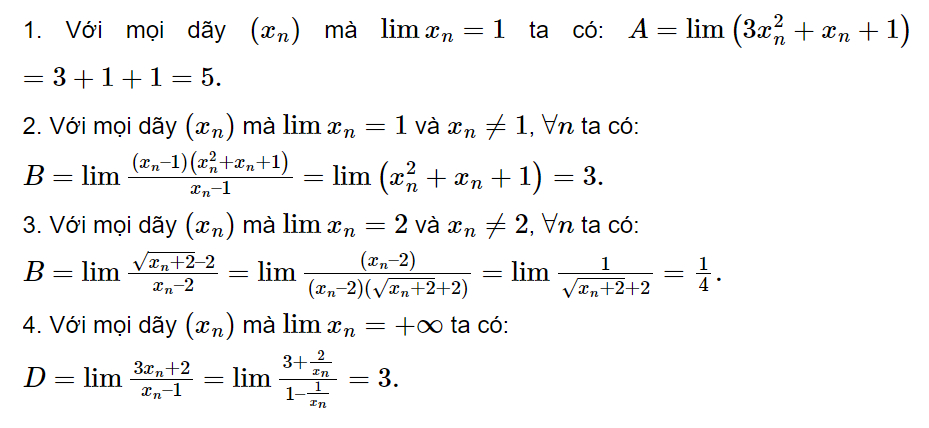
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Lim của một hằng số luôn bằng chính hằng số đó. Ví dụ, limx→a c = c, trong đó c là một hằng số bất kỳ và a là một số thực hoặc ∞.
Giải thích chi tiết về lim của hằng số
Định nghĩa
Giới hạn của một hàm số f(x) tại x = a được ký hiệu là limx→a f(x) và được hiểu là giá trị mà hàm số f(x) tiến gần tới khi x tiến gần tới a. Trong trường hợp f(x) là một hằng số c, thì giá trị của f(x) luôn bằng c bất kể x là bao nhiêu. Do đó, khi x tiến gần tới bất kỳ giá trị a nào, giá trị của f(x) vẫn luôn là c. Vì thế, limx→a c = c.Ví dụ minh họa
Hãy xét hàm số f(x) = 5. Dù x tiến đến bất kỳ giá trị nào (ví dụ: 0, 1, ∞, -∞), giá trị của f(x) luôn bằng 5. Do đó:- limx→0 5 = 5
- limx→1 5 = 5
- limx→∞ 5 = 5
- limx→-∞ 5 = 5
Ứng dụng
Hiểu được khái niệm lim của hằng số là nền tảng quan trọng để học các khái niệm giới hạn phức tạp hơn trong giải tích. Nó được sử dụng rộng rãi trong việc tính toán giới hạn của các hàm số, đạo hàm và tích phân. Việc nắm vững khái niệm này sẽ giúp bạn giải quyết các bài toán toán học một cách dễ dàng và chính xác hơn.Sản phẩm liên quan: mốt của mẫu số liệu
Xem thêm: pha nước chấm ốc luộc
Xem thêm: cách làm gạch cua bằng đậu phụ
Sản phẩm liên quan: nhiệt độ của nước đá đang tan
Sản phẩm liên quan: cách xóa gạch chân trong word