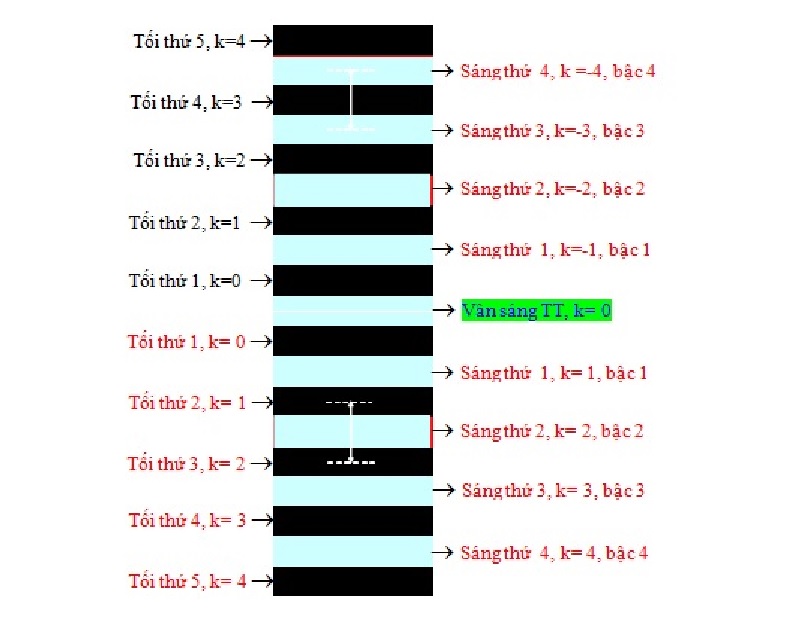
Khoảng cách giữa hai vân tối liên tiếp

Mô tả sản phẩm

Khoảng cách giữa hai vân tối liên tiếp trong hiện tượng giao thoa ánh sáng bằng khoảng cách giữa hai vân sáng liên tiếp và bằng i = λD/a, với λ là bước sóng ánh sáng, D là khoảng cách từ hai khe đến màn, và a là khoảng cách giữa hai khe.

Công thức tính khoảng cách giữa hai vân tối liên tiếp

Giải thích công thức

Khoảng cách giữa hai vân tối liên tiếp được tính bằng công thức: i = λD/a. Trong đó:

• λ (lambda): là bước sóng của ánh sáng sử dụng.
• D: là khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát.
• a: là khoảng cách giữa hai khe.

Công thức này được suy ra từ nguyên lý giao thoa ánh sáng, dựa trên sự chồng chập của các sóng ánh sáng từ hai khe. Vân tối xuất hiện tại các điểm mà hiệu đường đi của ánh sáng từ hai khe đến điểm đó là một số lẻ bán bước sóng ( (2k+1)λ/2 với k là số nguyên). Khoảng cách giữa hai vân tối liên tiếp tương ứng với sự thay đổi k thêm 1 đơn vị, dẫn đến công thức trên.

Ứng dụng của công thức

Công thức tính khoảng cách giữa hai vân tối liên tiếp có nhiều ứng dụng quan trọng trong:

• Đo bước sóng ánh sáng: Biết khoảng cách giữa hai vân tối, khoảng cách giữa hai khe và khoảng cách đến màn, ta có thể xác định bước sóng ánh sáng.
• Thiết kế các thiết bị quang học: Công thức này được sử dụng trong thiết kế các thiết bị quang học như máy giao thoa kế, kính hiển vi, v.v...
• Nghiên cứu các hiện tượng quang học: Hiểu rõ về giao thoa ánh sáng giúp chúng ta nghiên cứu và giải thích nhiều hiện tượng quang học khác.

Ví dụ minh họa

Giả sử ta có bước sóng ánh sáng λ = 500 nm, khoảng cách giữa hai khe a = 1 mm, khoảng cách từ hai khe đến màn D = 1 m. Khoảng cách giữa hai vân tối liên tiếp sẽ là: i = λD/a = (500 x 10^-9 m) x (1 m) / (1 x 10^-3 m) = 5 x 10^-4 m = 0.5 mm

Xem thêm: keo kẻ chỉ gạch

Xem thêm: n kí hiệu là gì trong vật lý

Sản phẩm hữu ích: ôn tập toán lớp 2 học kì 1

Sản phẩm hữu ích: cách tính det ma trận