Cách Tính Det Ma Trận

Mô tả sản phẩm

Để tính định thức (det) của một ma trận, ta cần xem xét kích thước của ma trận. Có nhiều phương pháp khác nhau tùy thuộc vào kích thước ma trận. Đối với ma trận 2x2, công thức rất đơn giản. Với ma trận có kích thước lớn hơn, ta có thể sử dụng phương pháp khai triển Laplace hoặc quy tắc Sarrus.

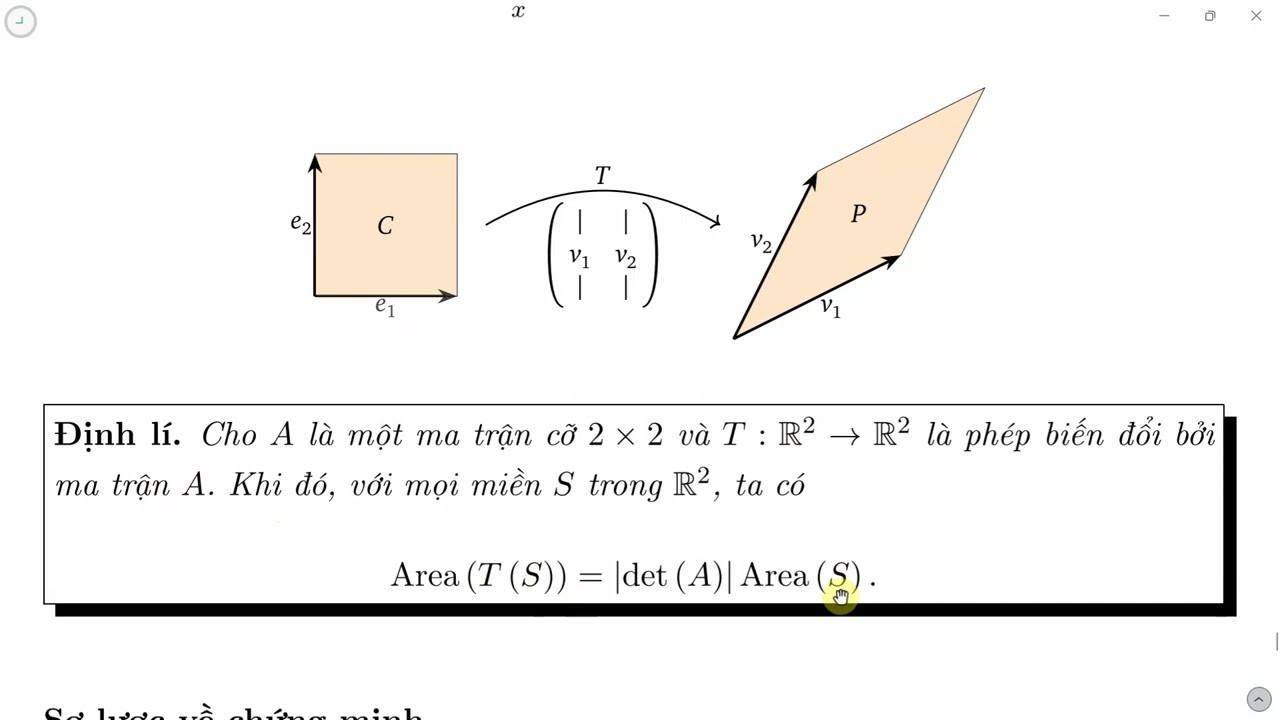
Tính Định Thức Ma Trận 2x2

Công thức:

Cho ma trận A = [[a, b], [c, d]], định thức của A (det(A)) được tính bằng công thức: det(A) = ad - bc. Ví dụ: nếu A = [[2, 3], [1, 4]], thì det(A) = (2*4) - (3*1) = 5.

Tính Định Thức Ma Trận 3x3

Phương pháp Quy tắc Sarrus:

Đối với ma trận 3x3, ta có thể sử dụng quy tắc Sarrus. Viết lại hai cột đầu tiên của ma trận sang bên phải. Tổng của tích các đường chéo chính trừ đi tổng của tích các đường chéo phụ sẽ cho ta định thức. Xem ví dụ minh họa cụ thể sẽ giúp bạn hiểu rõ hơn.

Phương pháp Khai Triển Laplace:

Phương pháp này áp dụng được cho ma trận có kích thước bất kỳ. Chọn một hàng hoặc một cột bất kỳ. Định thức sẽ bằng tổng của tích các phần tử trong hàng (hoặc cột) đó với phần bù đại số tương ứng. Phần bù đại số của một phần tử được tính bằng định thức của ma trận con thu được sau khi loại bỏ hàng và cột chứa phần tử đó, nhân với (-1)^(i+j), trong đó i và j là chỉ số hàng và cột của phần tử.

Tính Định Thức Ma Trận NxN (N > 3)

Phương pháp Khai Triển Laplace:

Đây là phương pháp hiệu quả nhất để tính định thức của ma trận có kích thước lớn hơn 3. Việc tính toán sẽ phức tạp hơn và thường cần sự trợ giúp của máy tính hoặc phần mềm toán học. Tóm lại, việc tính định thức ma trận phụ thuộc vào kích thước của ma trận. Đối với ma trận 2x2, công thức trực tiếp và dễ nhớ. Đối với ma trận lớn hơn, phương pháp khai triển Laplace là phương pháp tổng quát và hiệu quả. Hiểu rõ các phương pháp này sẽ giúp bạn giải quyết các bài toán liên quan đến ma trận một cách hiệu quả. Bạn có thể tìm hiểu thêm các ví dụ cụ thể trên mạng hoặc trong các tài liệu toán học để củng cố kiến thức.

Sản phẩm hữu ích: đã bao lần em vội vàng lạnh lùng làm ngơ

Xem thêm: tam giác vuông đều

Sản phẩm hữu ích: thau kinh hoi tu