Hình Tròn và Đường Tròn: Sự Khác Biệt và Điểm Chung

Mô tả sản phẩm

Hình tròn là một vùng kín được bao quanh bởi một đường tròn, trong khi đường tròn chỉ là tập hợp các điểm cách đều một điểm gọi là tâm. Sự khác biệt chính nằm ở việc hình tròn là một diện tích, còn đường tròn là một đường cong.

Sự khác biệt giữa hình tròn và đường tròn

Khái niệm

Hình tròn là một hình học phẳng bao gồm tất cả các điểm nằm trong một khoảng cách nhất định (bán kính) từ một điểm trung tâm. Đường tròn là đường cong khép kín bao gồm tất cả các điểm có cùng khoảng cách (bán kính) từ một điểm trung tâm. Hình tròn có diện tích, còn đường tròn không có diện tích, nó chỉ có chu vi.

Công thức tính toán

Diện tích hình tròn được tính bằng công thức: S = πr², trong đó r là bán kính. Chu vi đường tròn được tính bằng công thức: C = 2πr, trong đó r là bán kính. Như vậy, để tính toán hình tròn, ta cần tính diện tích, còn đối với đường tròn, ta cần tính chu vi.

Ứng dụng

Hình tròn và đường tròn được ứng dụng rộng rãi trong nhiều lĩnh vực, từ thiết kế kiến trúc, kỹ thuật, mỹ thuật cho đến các ngành khoa học tự nhiên. Ví dụ: bánh xe, đồng hồ, mặt trời, các loại hoa văn trang trí… đều liên quan đến hình tròn và đường tròn. Sự chính xác và tính đối xứng của hình tròn và đường tròn làm cho chúng trở nên lý tưởng cho nhiều ứng dụng thực tiễn.

Điểm chung giữa hình tròn và đường tròn

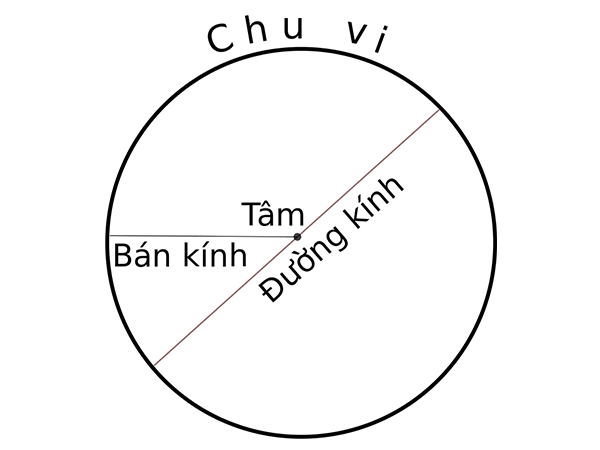
Tâm

Cả hình tròn và đường tròn đều có một điểm chung là tâm. Tâm là điểm nằm ở chính giữa, cách đều tất cả các điểm trên đường tròn.

Bán kính

Cả hình tròn và đường tròn đều được xác định bởi bán kính, đó là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn.

Ứng dụng trong toán học

Cả hình tròn và đường tròn đều là những khái niệm cơ bản và quan trọng trong toán học, được sử dụng để tính toán diện tích, chu vi và các đại lượng hình học khác. Chúng đóng vai trò quan trọng trong việc nghiên cứu hình học Euclid và các lĩnh vực toán học cao cấp hơn.

Xem thêm: cucl2 cộng gì ra cuoh2

Sản phẩm liên quan: tính từ bổ nghĩa cho gì

Sản phẩm liên quan: cách tính trung bình cộng của dãy số cách đều