Cách Tính Trung Bình Cộng Dãy Số Cách Đều
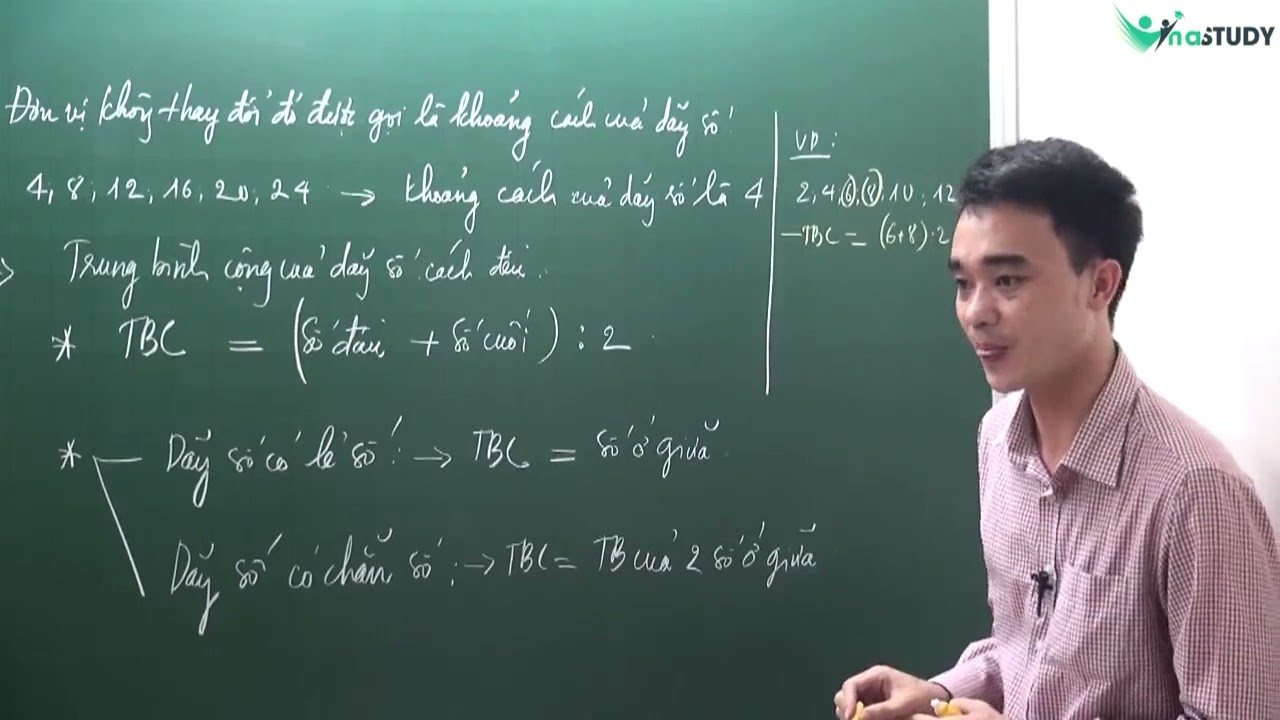


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Trung bình cộng của dãy số cách đều được tính bằng tổng các số trong dãy chia cho số lượng số hạng. Công thức đơn giản và nhanh chóng hơn có thể được áp dụng cho dãy số cách đều. Bạn chỉ cần lấy tổng của số hạng đầu tiên và số hạng cuối cùng, chia đôi, rồi nhân với số lượng số hạng.
Công thức tính trung bình cộng dãy số cách đều
Công thức tổng quát:
Trung bình cộng = (Số hạng đầu + Số hạng cuối) / 2 Công thức này áp dụng cho mọi dãy số cách đều, bất kể số lượng số hạng là bao nhiêu. Ví dụ, nếu bạn có dãy số 2, 4, 6, 8, 10, trung bình cộng sẽ là (2 + 10) / 2 = 6.Áp dụng công thức vào bài toán cụ thể:
Giả sử ta có dãy số cách đều: 1, 4, 7, 10, 13, 16. Đây là một dãy số cách đều với số hạng đầu là 1, số hạng cuối là 16 và công sai là 3. Để tính trung bình cộng, ta thực hiện như sau: 1. **Xác định số hạng đầu (a1) và số hạng cuối (an):** a1 = 1, an = 16 2. **Tính tổng số hạng (n):** Có 6 số hạng trong dãy số này (n = 6). 3. **Áp dụng công thức:** Trung bình cộng = (a1 + an) / 2 = (1 + 16) / 2 = 8.5 Như vậy, trung bình cộng của dãy số 1, 4, 7, 10, 13, 16 là 8.5.Lưu ý khi áp dụng công thức
Hãy nhớ rằng công thức này chỉ áp dụng cho các dãy số cách đều. Nếu dãy số không cách đều, bạn cần tính tổng tất cả các số hạng rồi chia cho số lượng số hạng để tìm trung bình cộng. Việc xác định chính xác số hạng đầu, số hạng cuối và số lượng số hạng là rất quan trọng để đảm bảo tính chính xác của kết quả.Sản phẩm hữu ích: thế nào là từ ghép phân loại
Xem thêm: tính chu vi đường tròn
Sản phẩm hữu ích: come out trong lgbt la gì
Xem thêm: bài thi viết chữ đẹp lớp 1 cấp huyện