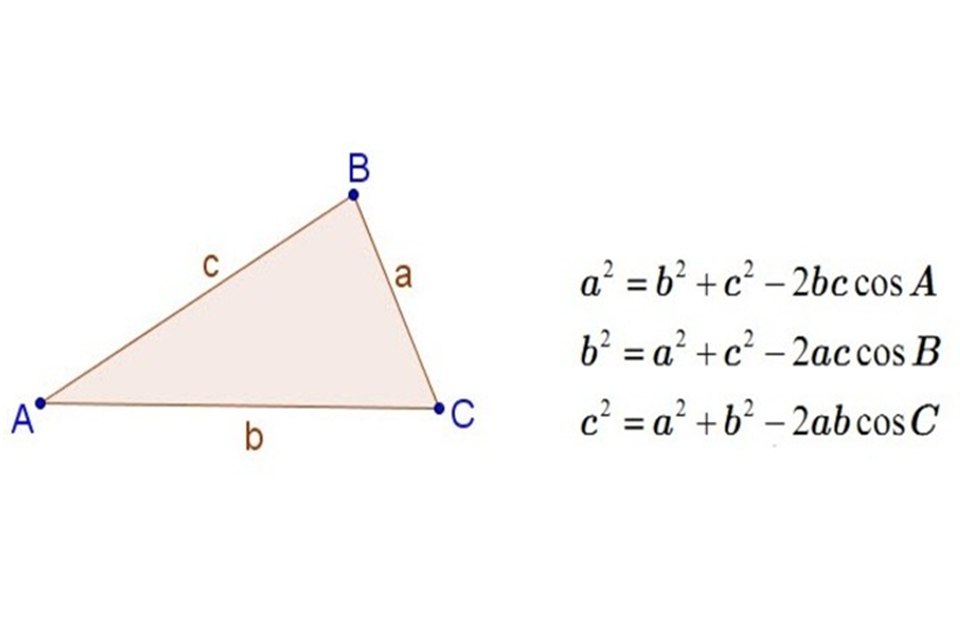
Hệ Quả Định Lý Cosin

Mô tả sản phẩm

Hệ quả của định lý cosin cho phép ta tính độ dài cạnh của một tam giác khi biết độ dài hai cạnh còn lại và góc xen giữa chúng, hoặc tính góc của tam giác khi biết độ dài ba cạnh. Điều này rất hữu ích trong nhiều ứng dụng thực tế và giải toán hình học.

Ứng dụng của Hệ Quả Định Lý Cosin

Tính độ dài cạnh tam giác:

Nếu biết độ dài hai cạnh a, b và góc C xen giữa chúng, ta có thể tính độ dài cạnh c bằng công thức: c² = a² + b² - 2ab cosC. Đây là một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến đo đạc, bản đồ, và xây dựng. Ví dụ, trong việc đo đạc khoảng cách giữa hai điểm không thể tiếp cận trực tiếp, người ta có thể sử dụng hệ quả này để tính toán khoảng cách đó.

Tính góc của tam giác:

Ngược lại, nếu biết độ dài ba cạnh a, b, c của tam giác, ta có thể tính cosin của một góc bất kỳ, ví dụ góc C, bằng công thức: cosC = (a² + b² - c²) / 2ab. Từ đó ta suy ra được số đo của góc C. Điều này rất hữu ích trong các bài toán hình học phức tạp, giúp xác định các góc chưa biết.

Ví dụ minh họa

Ví dụ 1: Tính độ dài cạnh

Giả sử ta có một tam giác ABC với AB = 5cm, AC = 7cm và góc BAC = 60°. Sử dụng hệ quả định lý cosin, ta có: BC² = 5² + 7² - 2(5)(7)cos60° = 25 + 49 - 35 = 39. Do đó, BC = √39 cm.

Ví dụ 2: Tính góc

Cho tam giác DEF với DE = 8cm, EF = 10cm và DF = 12cm. Ta có thể tính cos góc DEF bằng công thức: cos(DEF) = (8² + 12² - 10²) / (2 * 8 * 12) = 0.625. Vậy góc DEF = arccos(0.625) ≈ 51.32°. Hệ quả định lý cosin là một công cụ quan trọng trong hình học và có nhiều ứng dụng thực tế. Hiểu rõ và thành thạo hệ quả này sẽ giúp bạn giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Xem thêm: ca(oh)2 là oxit gì

Xem thêm: kỹ thuật bơi ếch cơ bản

Sản phẩm liên quan: bú cu giảng hòa