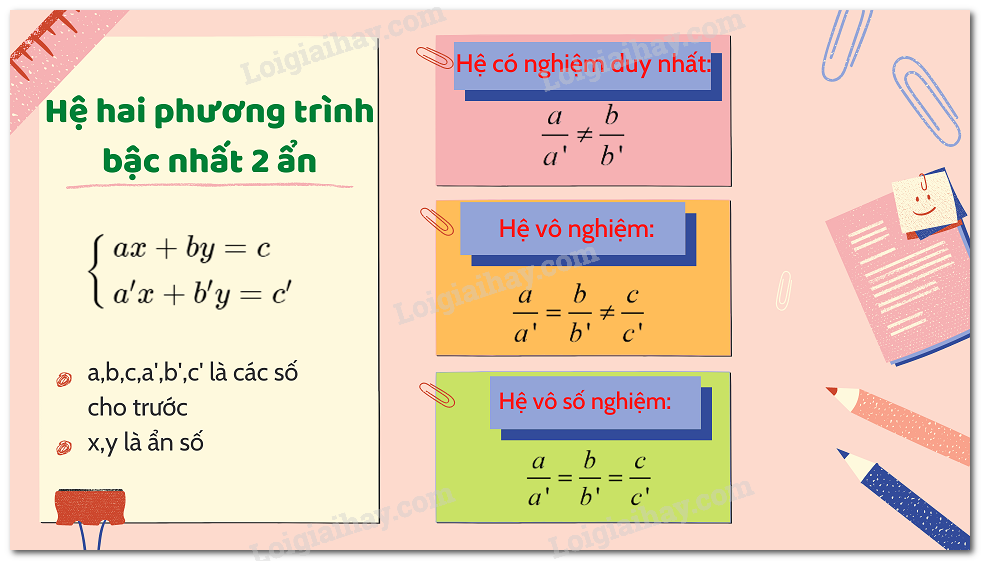
Hệ phương trình có nghiệm duy nhất khi nào?

Mô tả sản phẩm

Hệ phương trình tuyến tính có nghiệm duy nhất khi và chỉ khi định thức của ma trận hệ số khác 0. Điều này cũng tương đương với việc các vectơ cột (hoặc hàng) của ma trận hệ số là độc lập tuyến tính.

Hệ phương trình tuyến tính

Điều kiện cần và đủ

Hệ phương trình tuyến tính gồm m phương trình và n ẩn số có dạng:
a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁
a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂
...
a_m1x₁ + a_m2x₂ + ... + a_mnx_n = b_m
Hệ phương trình này có nghiệm duy nhất khi và chỉ khi:
1. Số phương trình bằng số ẩn (m = n): Điều này cần thiết nhưng chưa đủ để đảm bảo nghiệm duy nhất.
2. Định thức của ma trận hệ số khác 0 (det(A) ≠ 0): Đây là điều kiện đủ và cần thiết để hệ phương trình có nghiệm duy nhất. Ma trận hệ số A là ma trận gồm các hệ số a_ij.

Phương pháp kiểm tra

Để kiểm tra xem một hệ phương trình tuyến tính có nghiệm duy nhất hay không, bạn có thể sử dụng các phương pháp sau:
a) Tính định thức: Tính định thức của ma trận hệ số. Nếu định thức khác 0, hệ phương trình có nghiệm duy nhất.
b) Phương pháp khử Gauss: Sử dụng phương pháp khử Gauss để đưa ma trận hệ số về dạng bậc thang. Nếu sau khi khử, ta thu được ma trận tam giác trên với các phần tử trên đường chéo chính đều khác 0, thì hệ phương trình có nghiệm duy nhất.
c) Kiểm tra độc lập tuyến tính: Kiểm tra xem các vectơ cột (hoặc hàng) của ma trận hệ số có độc lập tuyến tính hay không. Nếu độc lập tuyến tính, hệ phương trình có nghiệm duy nhất.

Ví dụ minh họa

Xét hệ phương trình:
2x + y = 5
x - 2y = 1
Ma trận hệ số là: A = [[2, 1], [1, -2]]. Định thức của A là det(A) = (2)(-2) - (1)(1) = -5 ≠ 0. Do đó, hệ phương trình này có nghiệm duy nhất.

Kết luận

Tóm lại, một hệ phương trình tuyến tính có nghiệm duy nhất khi và chỉ khi định thức của ma trận hệ số khác 0. Điều này đảm bảo rằng hệ phương trình có một và chỉ một nghiệm duy nhất.

Sản phẩm liên quan: tập xác định của logarit

Sản phẩm hữu ích: 6li + n2 → 2li3n

Xem thêm: hệ sinh thái đặc trưng của đai cận nhiệt đới gió mùa trên núi

Sản phẩm hữu ích: amoniac có mùi gì