Tập xác định của logarit
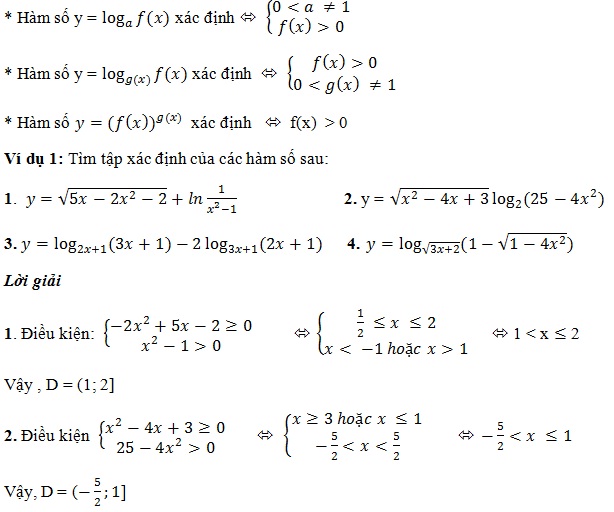


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tập xác định của hàm logarit y = logax (với a > 0, a ≠ 1) là tập hợp các số thực dương, tức là (0; +∞). Điều này có nghĩa là chỉ khi x > 0 thì hàm logarit mới có nghĩa.
Điều kiện xác định của hàm logarit
Tại sao tập xác định lại là (0; +∞)?
Điều kiện x > 0 xuất phát từ bản chất của logarit. Logarit cơ số a của x (logax) được định nghĩa là số mũ mà a phải được nâng lên để thu được x. Vì vậy, nếu x ≤ 0, thì không tồn tại số mũ nào có thể khiến amũ = x (với a > 0). Ví dụ, không thể tìm được số mũ nào để 2mũ = -1 hoặc 2mũ = 0. Do đó, để hàm số logarit có nghĩa, cơ số phải dương và khác 1, và đối số (x) phải luôn dương.
Ví dụ minh họa
Xét hàm số y = log2x. Tập xác định của hàm số này là (0; +∞). Điều này có nghĩa là chỉ những giá trị x lớn hơn 0 mới cho ta kết quả xác định. Nếu ta thay x = -1 hoặc x = 0 vào hàm số, ta sẽ không thu được giá trị nào cả.
Tập xác định của hàm logarit với cơ số và đối số phức tạp hơn
Trong trường hợp hàm logarit có dạng phức tạp hơn, ví dụ như y = loga(f(x)), việc tìm tập xác định cần thực hiện hai bước:
- Tìm điều kiện để f(x) > 0.
- Kết hợp điều kiện này với điều kiện a > 0 và a ≠ 1.
Sản phẩm liên quan: cách vẽ chân mày phẩy sợi
Sản phẩm hữu ích: cách xuất tin nhắn zalo ra file
Xem thêm: mất gốc hóa 8