Hàm số có đồ thị đối xứng qua trục tung
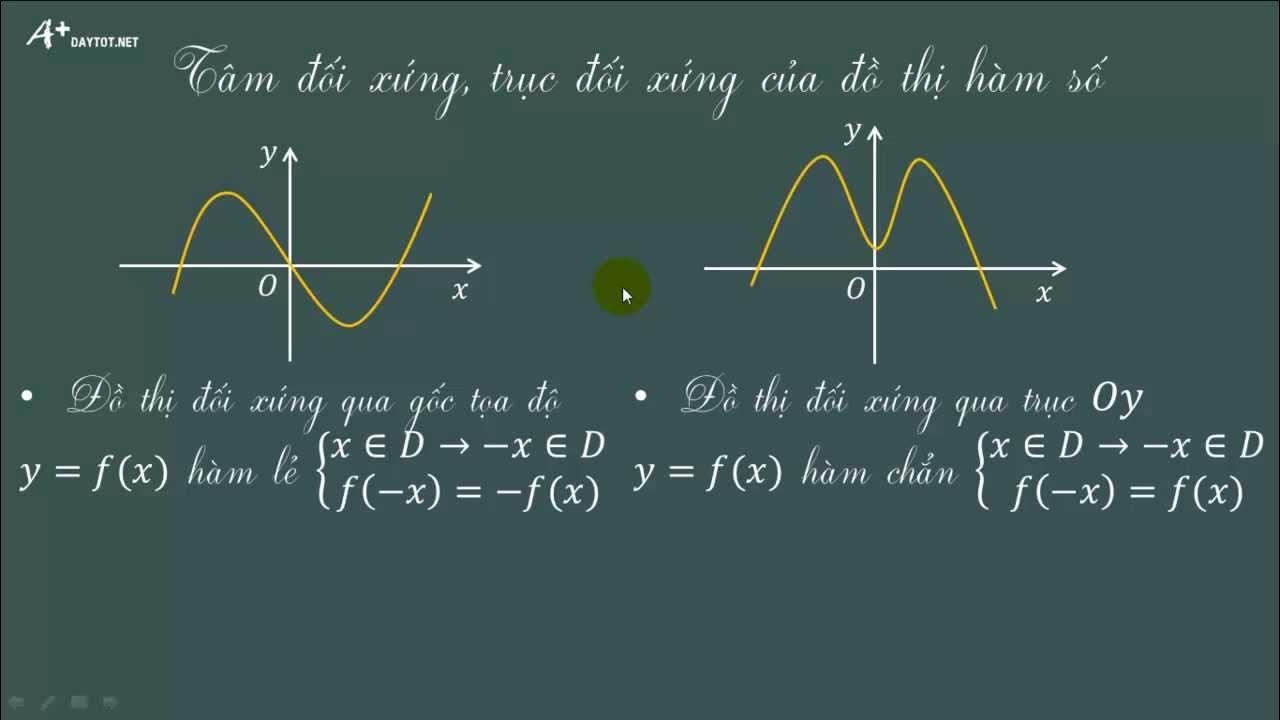
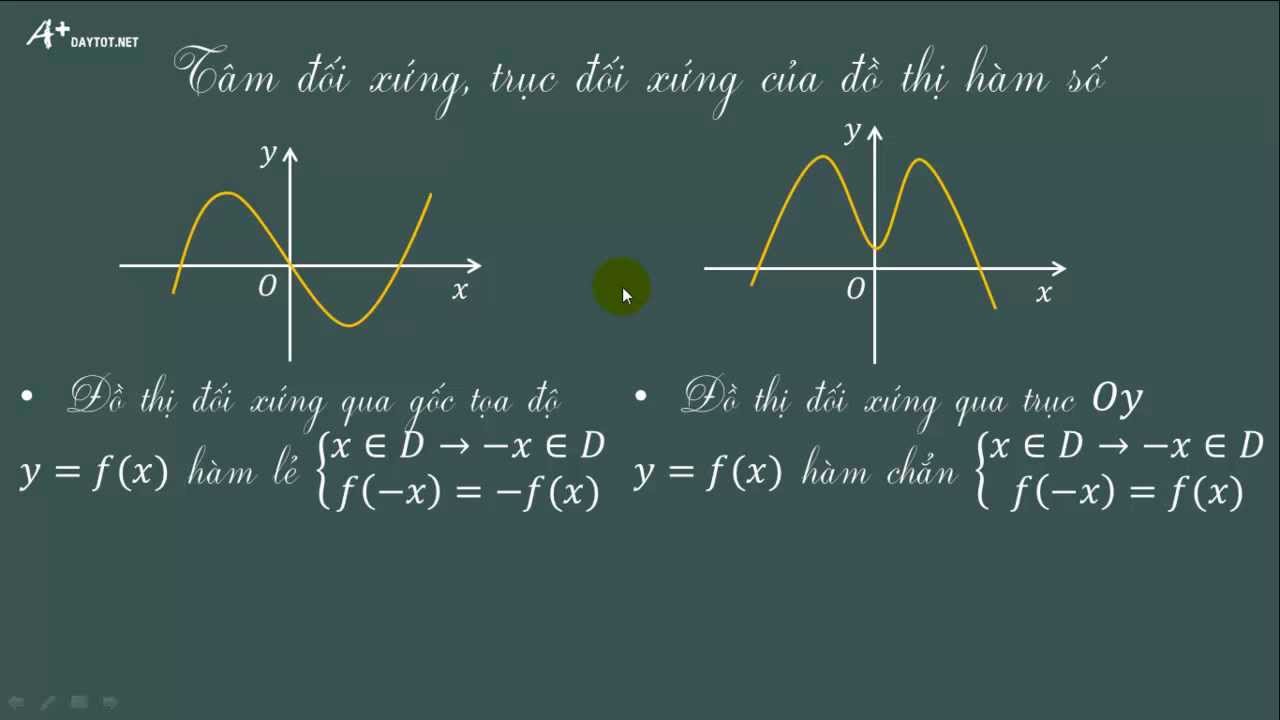
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Hàm số có đồ thị đối xứng qua trục tung là hàm số chẵn, nghĩa là f(x) = f(-x) với mọi x thuộc tập xác định. Điều này có nghĩa là nếu ta thay x bằng -x, giá trị của hàm số không thay đổi.
Đặc điểm của hàm số chẵn
Định nghĩa hàm số chẵn
Một hàm số f(x) được gọi là hàm số chẵn nếu và chỉ nếu f(x) = f(-x) với mọi x thuộc tập xác định của hàm số. Điều này dẫn đến đồ thị của hàm số chẵn đối xứng qua trục tung (Oy).Ví dụ về hàm số chẵn
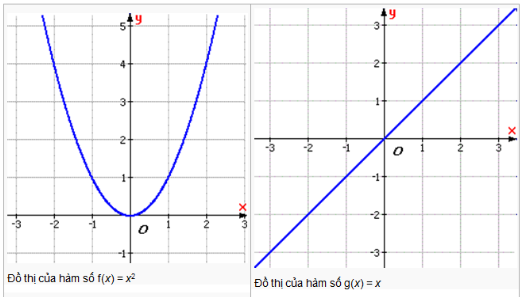
Ví dụ đơn giản nhất là hàm số f(x) = x². Ta có f(-x) = (-x)² = x² = f(x), do đó hàm số này là hàm số chẵn và đồ thị của nó là một parabol đối xứng qua trục tung. Các hàm số khác như f(x) = cos(x), f(x) = x⁴ cũng là hàm số chẵn.Cách xác định hàm số chẵn
Để xác định một hàm số có phải là hàm số chẵn hay không, ta cần thay x bởi -x vào biểu thức của hàm số. Nếu biểu thức thu được bằng với biểu thức ban đầu thì hàm số đó là hàm số chẵn. Nếu không, hàm số đó không phải là hàm số chẵn. Lưu ý rằng hàm số phải được xác định tại cả x và -x.Ứng dụng của hàm số chẵn
Hàm số chẵn có nhiều ứng dụng trong toán học và các lĩnh vực khác như vật lý, kỹ thuật. Việc hiểu tính chất đối xứng của đồ thị giúp đơn giản hóa việc vẽ đồ thị và phân tích các tính chất của hàm số. Trong lĩnh vực xử lý tín hiệu, hàm số chẵn đóng vai trò quan trọng trong việc phân tích tín hiệu.Sản phẩm liên quan: búp bê tấm cám
Xem thêm: ứng dụng của clorua vôi
Sản phẩm hữu ích: thư viện đề thi lớp 2
Sản phẩm liên quan: chữ nỉ trong tiếng trung