Đạo Hàm Cấp 1: Khái Niệm, Công Thức và Ví Dụ


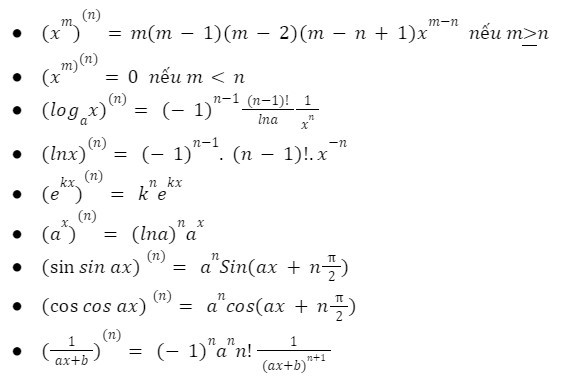
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Đạo hàm cấp 1 của một hàm số tại một điểm cho biết tốc độ thay đổi tức thời của hàm số tại điểm đó. Nói cách khác, nó biểu diễn độ dốc của đường tiếp tuyến của đồ thị hàm số tại điểm đó.
Khái niệm đạo hàm cấp 1
Định nghĩa
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 thuộc (a; b). Đạo hàm cấp 1 của hàm số f(x) tại điểm x0, ký hiệu là f'(x0) hoặc y'(x0), được định nghĩa là: f'(x0) = limx→x0 [(f(x) - f(x0)) / (x - x0)] (nếu giới hạn này tồn tại).
Ý nghĩa hình học
Đạo hàm cấp 1 tại một điểm chính là hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm đó. Điều này giúp ta hiểu được hướng và tốc độ thay đổi của hàm số tại điểm đó.
Công thức đạo hàm cấp 1 của một số hàm số cơ bản
Các hàm cơ bản và đạo hàm
Dưới đây là bảng đạo hàm của một số hàm số cơ bản thường gặp:
- y = xn => y' = nxn-1
- y = sinx => y' = cosx
- y = cosx => y' = -sinx
- y = ex => y' = ex
- y = ax => y' = axln(a)
- y = ln(x) => y' = 1/x
- y = loga(x) => y' = 1/(xln(a))
Ví dụ về đạo hàm cấp 1
Tính đạo hàm của hàm số y = x² + 2x + 1
Áp dụng công thức đạo hàm, ta có: y' = 2x + 2
Ứng dụng của đạo hàm cấp 1
Đạo hàm cấp 1 có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác như vật lý, kinh tế. Ví dụ, nó được sử dụng để tìm cực trị của hàm số, tìm điểm uốn, giải các bài toán tối ưu hóa.
Xem thêm: nêu cấu tạo và nguyên lý làm việc của động cơ điện một pha
Sản phẩm liên quan: xem cặp câu hỏi và trả lời đầu tiên tìm được
Sản phẩm hữu ích: cách trị dày sừng nang lông