Công thức tính độ lệch chuẩn
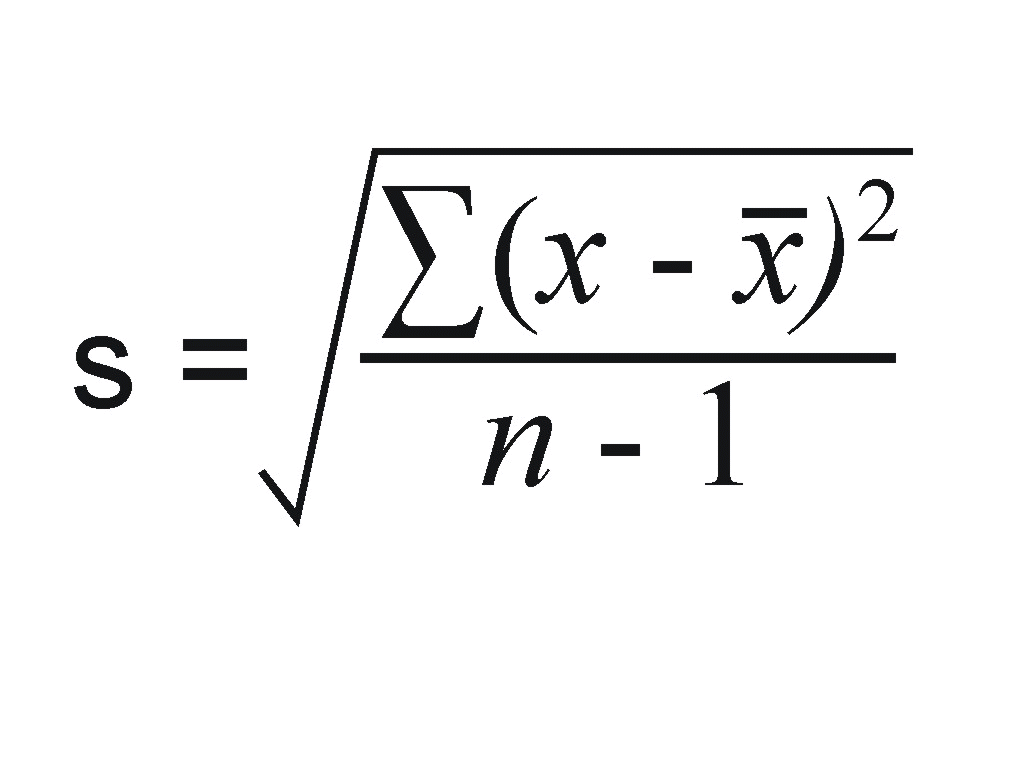


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính độ lệch chuẩn phụ thuộc vào việc bạn đang tính độ lệch chuẩn mẫu hay độ lệch chuẩn toàn bộ quần thể. Đối với mẫu, công thức là: √[Σ(xi - x̄)² / (n - 1)], trong đó xi là mỗi giá trị dữ liệu, x̄ là trung bình mẫu, và n là số lượng dữ liệu trong mẫu. Đối với toàn bộ quần thể, công thức là: √[Σ(xi - μ)² / N], trong đó μ là trung bình toàn bộ quần thể và N là tổng số dữ liệu trong quần thể.
Hiểu rõ các khái niệm trong công thức
Trung bình mẫu (x̄) và Trung bình quần thể (μ)
Trung bình mẫu (x̄) là tổng của tất cả các giá trị dữ liệu trong mẫu, chia cho số lượng dữ liệu trong mẫu. Trung bình quần thể (μ) là tổng của tất cả các giá trị dữ liệu trong toàn bộ quần thể, chia cho tổng số dữ liệu trong quần thể. Đây là bước đầu tiên và quan trọng để tính độ lệch chuẩn.
Độ lệch bình phương (Σ(xi - x̄)² hoặc Σ(xi - μ)²)
Đây là tổng của bình phương các độ lệch của mỗi giá trị dữ liệu so với trung bình mẫu (x̄) hoặc trung bình quần thể (μ). Bước này đo lường mức độ phân tán của dữ liệu quanh trung bình.
Số lượng dữ liệu (n và N)
n là kích thước mẫu (số lượng dữ liệu trong mẫu), còn N là kích thước quần thể (tổng số dữ liệu trong quần thể). Việc sử dụng n-1 trong công thức độ lệch chuẩn mẫu là để điều chỉnh độ lệch, làm cho ước lượng độ lệch chuẩn mẫu chính xác hơn khi áp dụng cho quần thể lớn hơn.
Ứng dụng của độ lệch chuẩn
Độ lệch chuẩn là một chỉ số thống kê quan trọng được sử dụng rộng rãi trong nhiều lĩnh vực, giúp đo lường sự phân tán của dữ liệu quanh giá trị trung bình. Một độ lệch chuẩn nhỏ cho thấy dữ liệu tập trung quanh trung bình, trong khi một độ lệch chuẩn lớn cho thấy dữ liệu phân tán rộng rãi hơn.
Ví dụ minh họa
Giả sử ta có một mẫu gồm các giá trị: 2, 4, 4, 4, 5, 5, 7, 9. Để tính độ lệch chuẩn mẫu, ta thực hiện các bước sau:
- Tính trung bình mẫu (x̄): (2 + 4 + 4 + 4 + 5 + 5 + 7 + 9) / 8 = 5
- Tính độ lệch bình phương: (2-5)² + (4-5)² + (4-5)² + (4-5)² + (5-5)² + (5-5)² + (7-5)² + (9-5)² = 28
- Chia tổng độ lệch bình phương cho n-1: 28 / (8 - 1) = 4
- Tính căn bậc hai của kết quả: √4 = 2
Sản phẩm hữu ích: viết các công thức
Xem thêm: oxit axit có thể tác dụng được với
Xem thêm: phương trình dao động của vật
Sản phẩm hữu ích: rượu etylic trong phân tử gồm