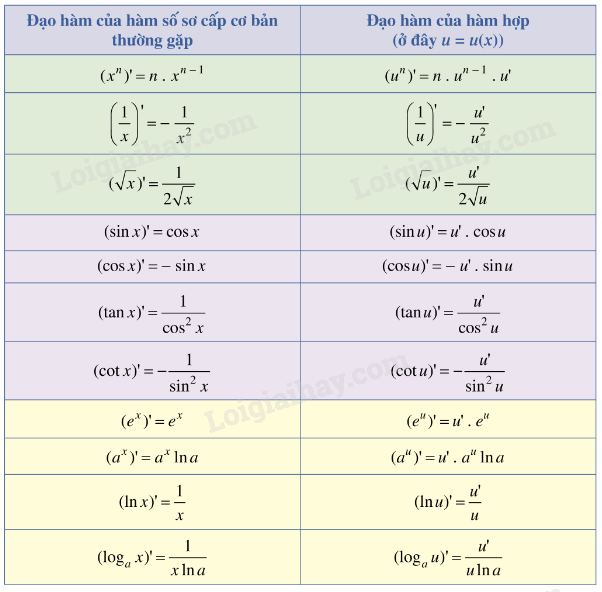
Công thức tính đạo hàm của hàm số

Mô tả sản phẩm

Công thức tính đạo hàm của hàm số phụ thuộc vào dạng hàm số. Có nhiều công thức đạo hàm khác nhau cho các hàm số khác nhau. Bài viết này sẽ tóm tắt các công thức đạo hàm cơ bản và cách áp dụng chúng.

Đạo hàm của các hàm số cơ bản

Đạo hàm của hàm hằng số:

Nếu y = c (c là hằng số), thì y' = 0.

Đạo hàm của hàm số lũy thừa:

Nếu y = xⁿ (n là số thực), thì y' = nx^n-1. Ví dụ: đạo hàm của x² là 2x, đạo hàm của x^1/2 (hay √x) là (1/2)x^-1/2 = 1/(2√x).

Đạo hàm của hàm số mũ:

Nếu y = a^x (a > 0, a ≠ 1), thì y' = a^xln(a). Đặc biệt, nếu y = e^x, thì y' = e^x.

Đạo hàm của hàm số logarit:

Nếu y = log_ax (a > 0, a ≠ 1), thì y' = 1/(xln(a)). Đặc biệt, nếu y = ln(x), thì y' = 1/x.

Đạo hàm của hàm số lượng giác:

* Nếu y = sin(x), thì y' = cos(x). * Nếu y = cos(x), thì y' = -sin(x). * Nếu y = tan(x), thì y' = 1/cos²(x) = sec²(x). * Nếu y = cot(x), thì y' = -1/sin²(x) = -csc²(x).

Các quy tắc đạo hàm

Quy tắc đạo hàm của tổng và hiệu:

(u ± v)' = u' ± v'

Quy tắc đạo hàm của tích:

(uv)' = u'v + uv'

Quy tắc đạo hàm của thương:

(u/v)' = (u'v - uv')/v² (v ≠ 0)

Quy tắc đạo hàm hàm hợp:

Nếu y = f(g(x)), thì y' = f'(g(x)) * g'(x). Việc hiểu và áp dụng thành thạo các công thức và quy tắc đạo hàm trên sẽ giúp bạn giải quyết được nhiều bài toán liên quan đến đạo hàm trong toán học và các lĩnh vực ứng dụng khác. Hãy luyện tập thường xuyên để nâng cao kỹ năng của mình.

Xem thêm: quy tắc bàn tay trái lớp 11

Xem thêm: công thức tính cos trong tam giác

Sản phẩm hữu ích: dầu mỏ khí đốt có tiềm năng và triển vọng lớn của nước ta tập trung ở

Xem thêm: so sánh tính dẫn nhiệt của các chất