Công thức tính Cos trong Tam giác

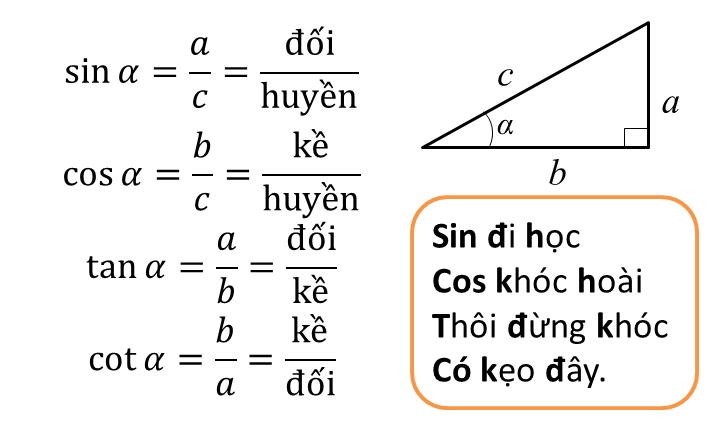
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính cos trong tam giác được sử dụng để tính độ dài cạnh hoặc góc của một tam giác khi biết các thông tin khác. Có nhiều công thức khác nhau tùy thuộc vào dữ liệu đã biết.
Công thức Cos trong Tam giác bất kỳ
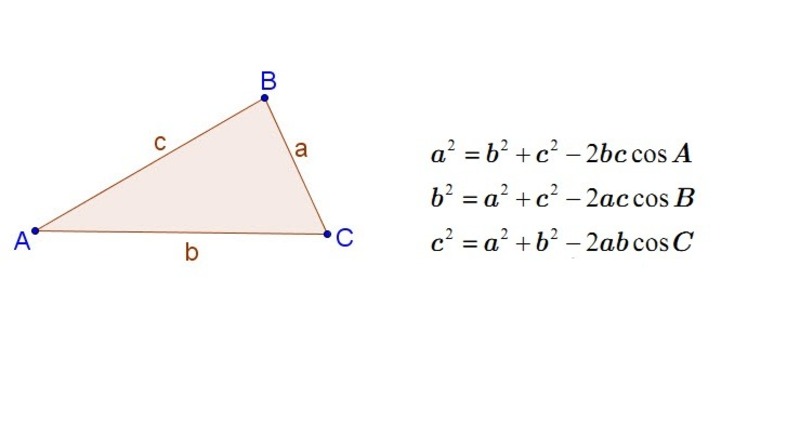
Định lý Cosin
Định lý Cosin là công thức cơ bản nhất để tính cosin của một góc trong tam giác bất kỳ. Cho tam giác ABC với độ dài các cạnh a, b, c lần lượt đối diện với các góc A, B, C, ta có:
- a² = b² + c² - 2bc cosA
- b² = a² + c² - 2ac cosB
- c² = a² + b² - 2ab cosC
Từ các công thức trên, ta có thể suy ra công thức tính cosin của mỗi góc:
- cosA = (b² + c² - a²) / 2bc
- cosB = (a² + c² - b²) / 2ac
- cosC = (a² + b² - c²) / 2ab
Công thức này áp dụng được cho mọi loại tam giác, kể cả tam giác nhọn, tam giác tù và tam giác vuông.
Công thức Cos trong Tam giác vuông
Tỉ số lượng giác
Trong tam giác vuông, ta có thể sử dụng tỉ số lượng giác để tính cosin của một góc nhọn. Cho tam giác vuông ABC vuông tại A, ta có:
- cosB = AB/BC (cạnh kề/cạnh huyền)
- cosC = AC/BC (cạnh kề/cạnh huyền)
Trong đó: AB là cạnh kề góc B, AC là cạnh kề góc C, BC là cạnh huyền.
Ứng dụng của công thức tính Cos trong tam giác
Công thức tính cos trong tam giác có nhiều ứng dụng thực tiễn quan trọng trong các lĩnh vực như: đo đạc, xây dựng, hàng hải, hàng không, lập trình đồ họa… Việc hiểu và áp dụng thành thạo các công thức này giúp giải quyết nhiều bài toán liên quan đến hình học phẳng.
Sản phẩm liên quan: vai trò nguyên tố vi lượng
Sản phẩm hữu ích: điện trở đơn vị là gì
Xem thêm: chất chỉ thị axit bazơ
Sản phẩm liên quan: động năng cực đại