Công thức khoảng cách giữa hai mặt phẳng

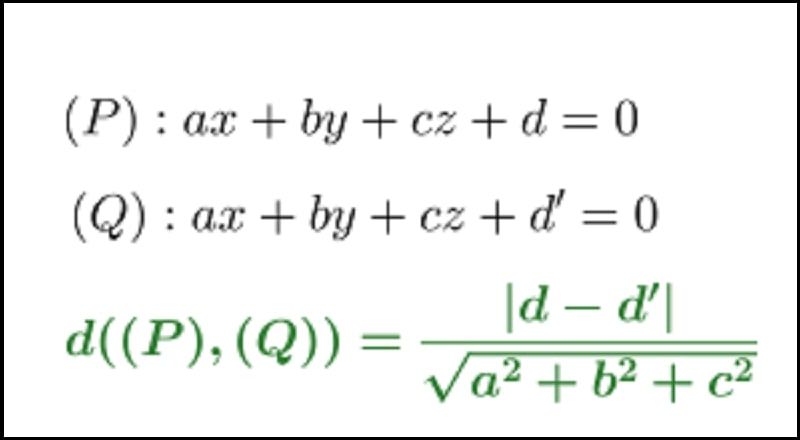
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Khoảng cách giữa hai mặt phẳng song song được tính bằng công thức: d = |D - D'| / √(A² + B² + C²), trong đó (A, B, C) là các hệ số của phương trình mặt phẳng và D, D' là các hệ số tự do.
Công thức tính khoảng cách giữa hai mặt phẳng song song
Trường hợp tổng quát
Cho hai mặt phẳng song song (P) và (Q) có phương trình tổng quát lần lượt là:
Ax + By + Cz + D = 0
Ax + By + Cz + D' = 0
trong đó A, B, C không đồng thời bằng 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) được tính theo công thức:
d((P), (Q)) = |D - D'| / √(A² + B² + C²)
Trong đó: |D - D'| là giá trị tuyệt đối của hiệu số giữa hai hệ số tự do D và D'. √(A² + B² + C²) là độ dài vectơ pháp tuyến của mặt phẳng.
Ví dụ minh họa
Cho hai mặt phẳng:
2x + 3y - z + 4 = 0
2x + 3y - z - 1 = 0
Khoảng cách giữa hai mặt phẳng là:
d = |4 - (-1)| / √(2² + 3² + (-1)²) = 5 / √14
Lưu ý
Công thức trên chỉ áp dụng cho trường hợp hai mặt phẳng song song. Nếu hai mặt phẳng không song song, khoảng cách giữa chúng sẽ phụ thuộc vào điểm được chọn trên mỗi mặt phẳng. Trong trường hợp này, cần tìm một đường thẳng vuông góc với cả hai mặt phẳng và tính khoảng cách giữa giao điểm của đường thẳng đó với mỗi mặt phẳng.
Công thức này rất hữu ích trong việc giải toán hình học không gian, đặc biệt là trong các bài toán liên quan đến vị trí tương đối của các mặt phẳng.
Xem thêm: giải vở bài tập toán lớp 3 chân trời sáng tạo
Sản phẩm hữu ích: vừa mới tiếng anh
Xem thêm: cv kế toán tiếng anh
Xem thêm: tiếng chim họa mi