Công thức khai triển nhị thức Newton
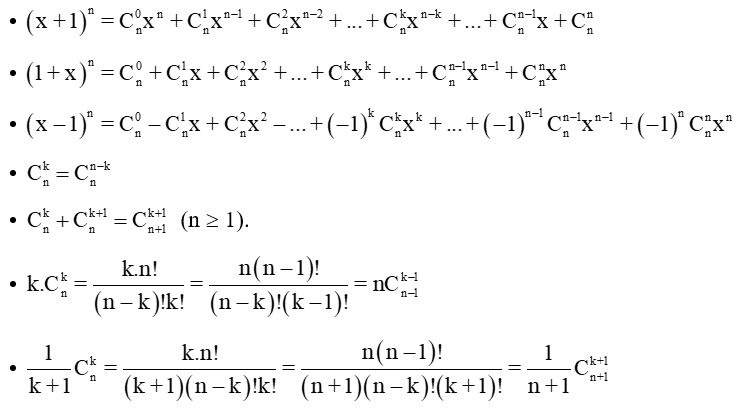
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức khai triển nhị thức Newton cho phép ta khai triển một biểu thức dạng (a + b)n thành một đa thức, với n là một số nguyên không âm. Công thức này rất hữu ích trong toán học, vật lý và nhiều lĩnh vực khác.
Công thức tổng quát
Định nghĩa
Công thức khai triển nhị thức Newton được viết như sau: (a + b)n = Σk=0n (nCk) * an-k * bk, trong đó nCk là tổ hợp chập k của n phần tử, được tính bằng n! / (k! * (n-k)!).Ví dụ minh họa
Hãy xét ví dụ (x + y)3. Áp dụng công thức khai triển nhị thức Newton, ta có: (x + y)3 = 3C0 * x3 * y0 + 3C1 * x2 * y1 + 3C2 * x1 * y2 + 3C3 * x0 * y3 = x3 + 3x2y + 3xy2 + y3Ứng dụng của công thức khai triển nhị thức Newton
Công thức khai triển nhị thức Newton có rất nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:Toán học
* Tính toán tổ hợp và xác suất. * Giải phương trình và bất phương trình. * Xấp xỉ các hàm số.Vật lý
* Mô hình hóa các hiện tượng vật lý. * Tính toán các đại lượng vật lý.Tin học
* Thiết kế thuật toán. * Phân tích độ phức tạp của thuật toán.Tổng kết
Công thức khai triển nhị thức Newton là một công cụ mạnh mẽ trong toán học và các lĩnh vực liên quan. Hiểu rõ công thức này và cách áp dụng nó sẽ giúp bạn giải quyết nhiều bài toán phức tạp một cách hiệu quả.Sản phẩm hữu ích: trắc nghiệm toán lớp 2 giữa kì 1
Sản phẩm liên quan: trục đối xứng của đồ thị hàm số
Xem thêm: giáo án nhận biết hình tròn hình tam giác
Sản phẩm hữu ích: vẽ về mùa xuân
Sản phẩm liên quan: luyện ngón bàn phím