Trục Đối Xứng của Đồ Thị Hàm Số
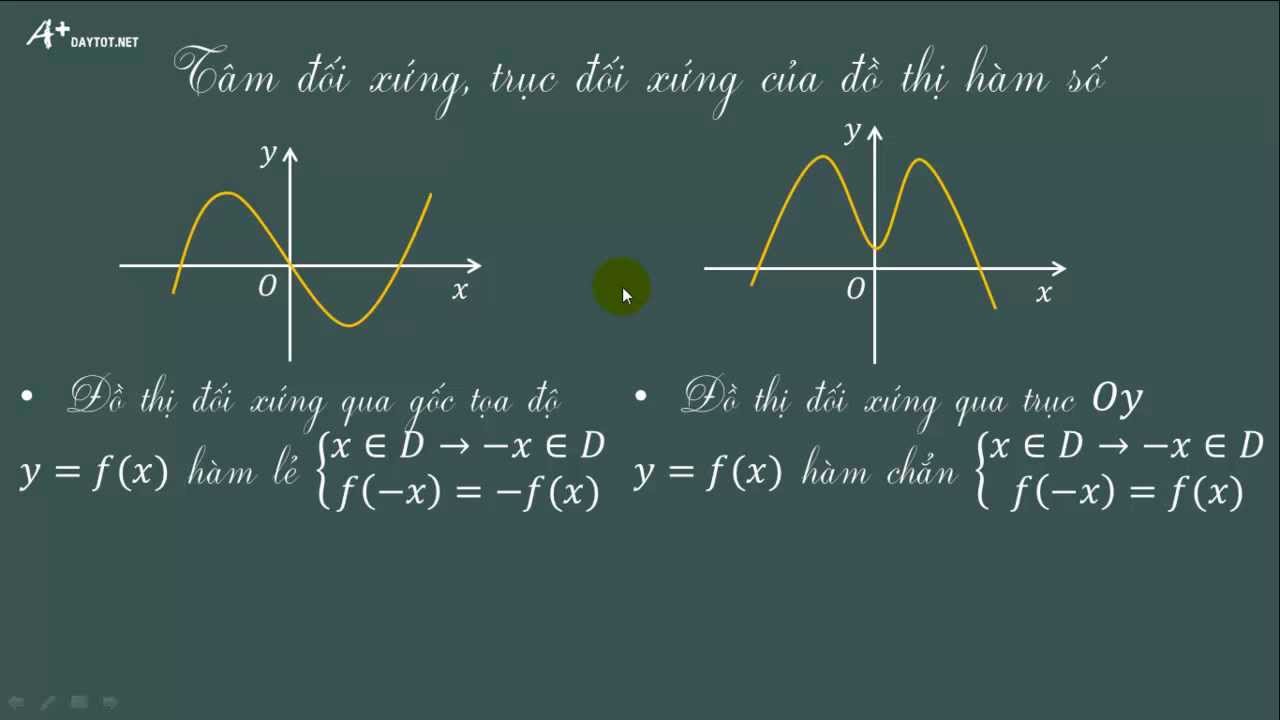
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
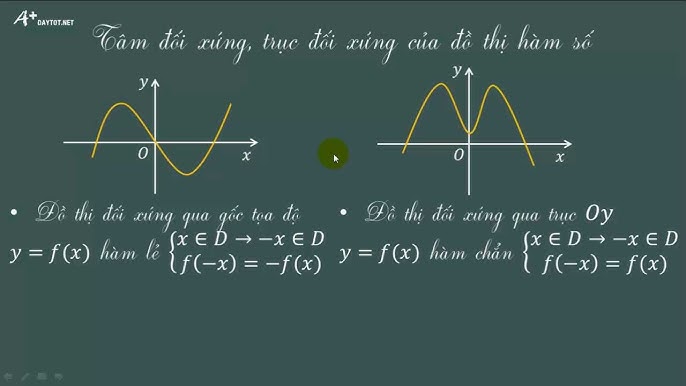
Trục đối xứng của đồ thị hàm số là đường thẳng mà khi ta "gập" đồ thị theo đường thẳng đó, hai nửa đồ thị sẽ trùng khít lên nhau. Vị trí của trục đối xứng phụ thuộc vào dạng hàm số.
Tìm Trục Đối Xứng của Hàm Số Bậc Hai
Công thức tổng quát và trục đối xứng
Đối với hàm số bậc hai có dạng tổng quát y = ax² + bx + c (với a ≠ 0), trục đối xứng là đường thẳng đứng có phương trình x = -b/(2a). Đây là một công thức quan trọng và dễ nhớ để xác định trục đối xứng của parabol.
Ví dụ minh họa
Cho hàm số y = 2x² + 4x - 3. Ta có a = 2, b = 4, c = -3. Vậy trục đối xứng là x = -4/(2*2) = -1. Điều này có nghĩa là đường thẳng x = -1 là trục đối xứng của parabol này.
Trục Đối Xứng của các Hàm Số Khác
Hàm số khác
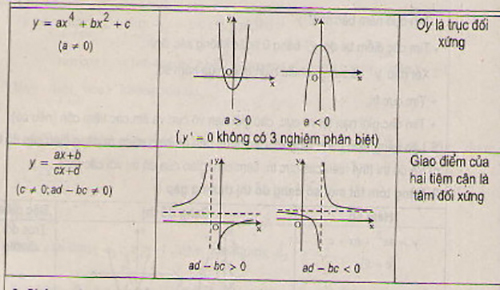
Không phải tất cả các hàm số đều có trục đối xứng. Ví dụ, hàm số bậc ba, hàm số mũ, hàm số logarit thường không có trục đối xứng. Tuy nhiên, một số hàm số đặc biệt có thể có trục đối xứng khác, tùy thuộc vào dạng của hàm số. Việc xác định trục đối xứng trong trường hợp này thường phức tạp hơn và đòi hỏi kỹ thuật toán học cao hơn.
Tìm hiểu sâu hơn
Để hiểu rõ hơn về trục đối xứng của đồ thị hàm số, bạn nên tìm hiểu thêm về các khái niệm liên quan như đỉnh parabol, tính chẵn lẻ của hàm số và các phương pháp đồ thị hàm số. Việc vẽ đồ thị hàm số cũng giúp trực quan hóa vị trí của trục đối xứng.
Sản phẩm hữu ích: cằn cỗi là gì
Xem thêm: hóa chất tinh khiết
Sản phẩm hữu ích: andehit axetic + agno3
Sản phẩm liên quan: 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d 7p
Sản phẩm liên quan: mùa xuân xanh đọc hiểu