Công thức hạ bậc nâng cung
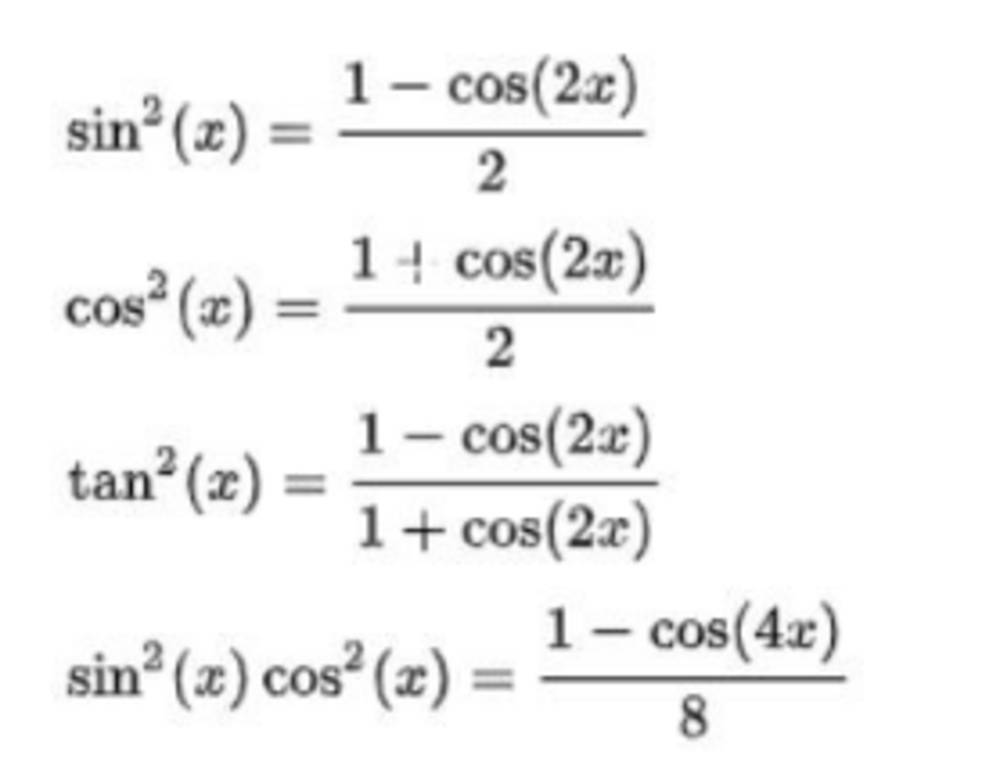
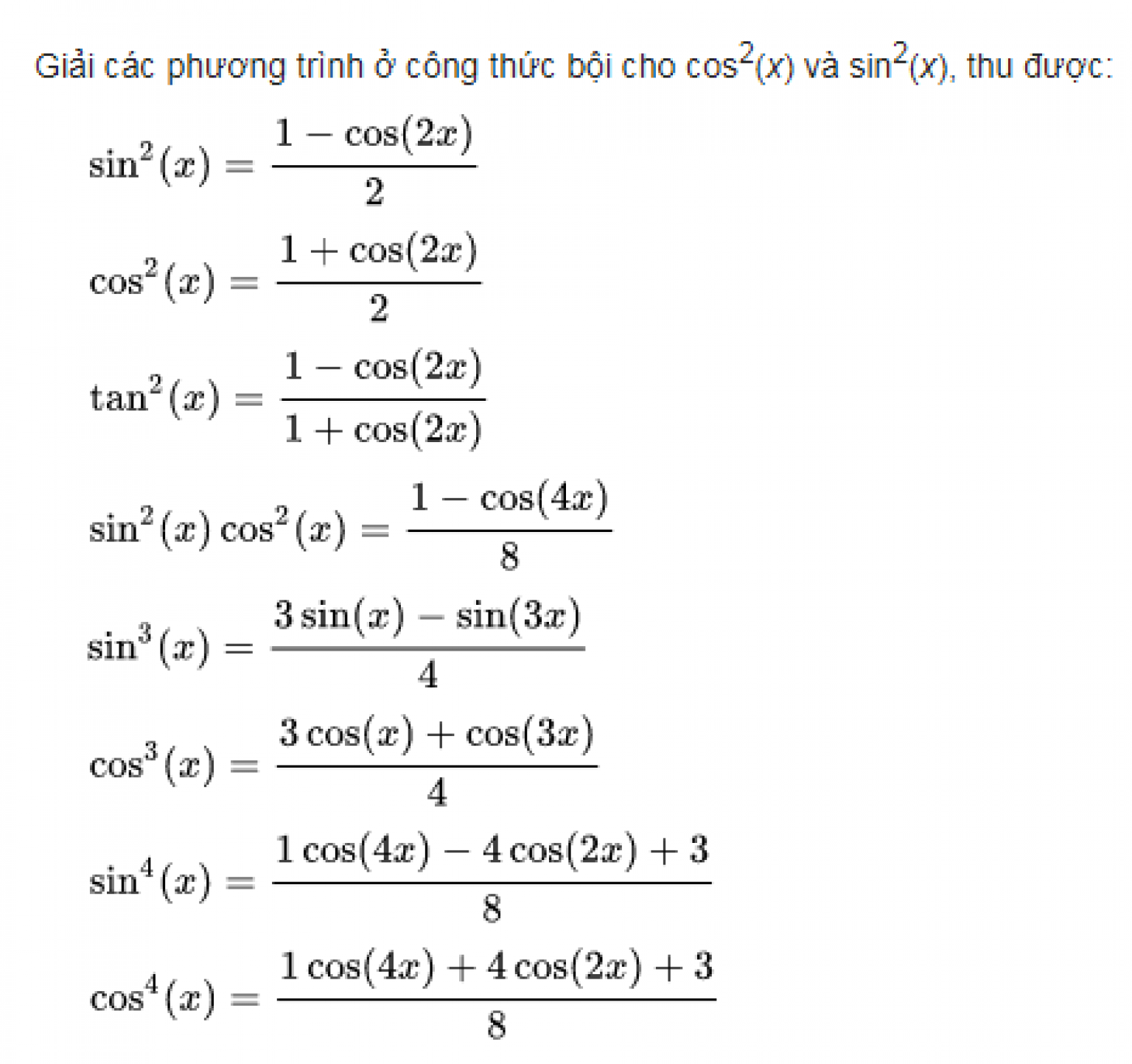

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức hạ bậc và nâng cung trong lượng giác giúp biến đổi các biểu thức lượng giác phức tạp thành các biểu thức đơn giản hơn, dễ tính toán hơn. Chúng thường được sử dụng để giải phương trình lượng giác, tính tích phân và đơn giản hóa các biểu thức lượng giác trong các bài toán toán học và vật lý.
Công thức hạ bậc
Hạ bậc các hàm lượng giác cơ bản:
- sin2x = (1 - cos2x)/2
- cos2x = (1 + cos2x)/2
- tan2x = (1 - cos2x)/(1 + cos2x)
Những công thức này giúp chuyển đổi bình phương của các hàm lượng giác thành hàm cosin của góc gấp đôi. Điều này rất hữu ích khi giải các phương trình lượng giác hoặc đơn giản hóa các biểu thức phức tạp.
Ứng dụng của công thức hạ bậc:
Công thức hạ bậc được ứng dụng rộng rãi trong việc tính tích phân chứa hàm lượng giác, giải phương trình lượng giác, chứng minh các đẳng thức lượng giác và đơn giản hóa các biểu thức phức tạp trong các bài toán toán học và vật lý.
Công thức nâng cung
Nâng cung các hàm lượng giác cơ bản:
- sin2x = 2sinxcosx
- cos2x = cos2x - sin2x = 2cos2x - 1 = 1 - 2sin2x
- tan2x = (2tanx)/(1 - tan2x)
Công thức nâng cung cho phép biểu diễn hàm lượng giác của góc gấp đôi thông qua các hàm lượng giác của góc đơn. Điều này hữu ích trong việc giải phương trình lượng giác và biến đổi các biểu thức lượng giác.
Ứng dụng của công thức nâng cung:
Công thức nâng cung được sử dụng rộng rãi trong giải phương trình lượng giác, rút gọn biểu thức lượng giác, tính toán các giá trị lượng giác của góc gấp đôi và trong nhiều ứng dụng khác trong toán học và vật lý.
Việc thành thạo các công thức hạ bậc và nâng cung là rất quan trọng đối với việc giải quyết các bài toán liên quan đến lượng giác. Hiểu rõ cách sử dụng chúng sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và hiệu quả hơn.
Sản phẩm hữu ích: vẽ trọng tâm tam giác
Xem thêm: tổng hợp các dạng toán nâng cao lớp 3 có đáp an
Sản phẩm hữu ích: con gì đầu dê mình ốc
Xem thêm: để phương trình có 2 nghiệm
Sản phẩm hữu ích: cách nhận biết phi kim và kim loại