Chứng minh Định lý Napoleon
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
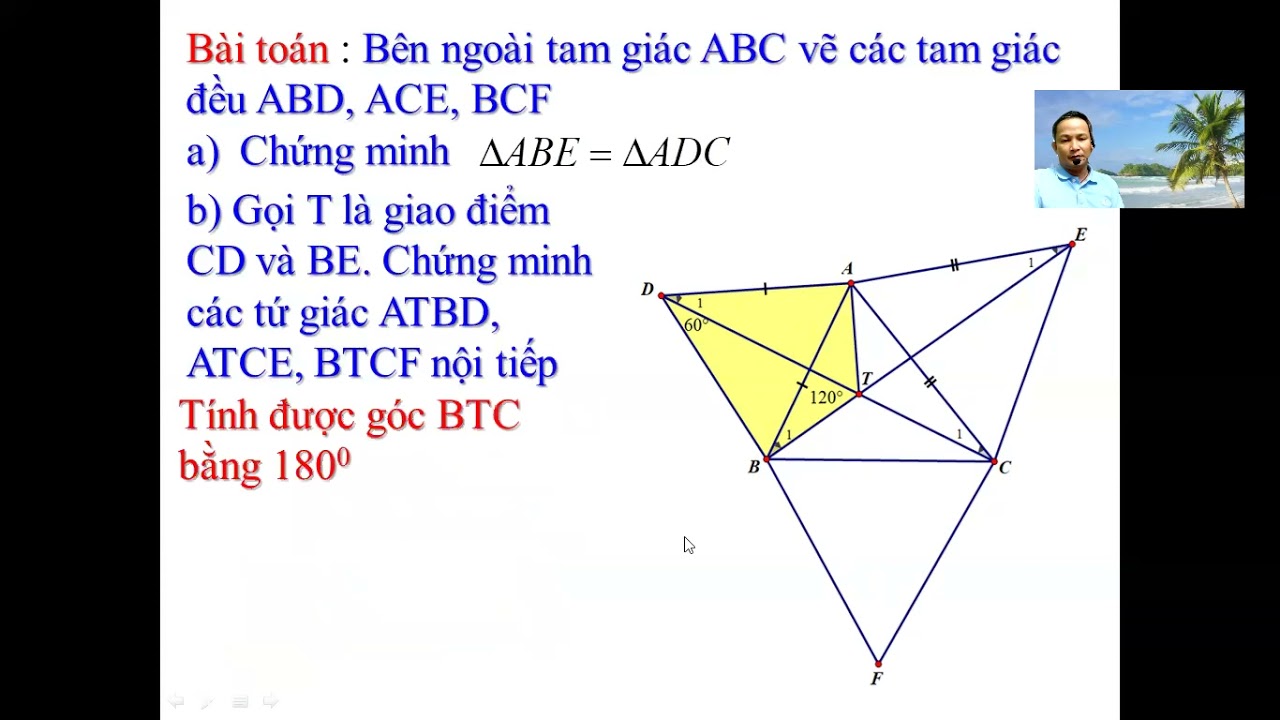
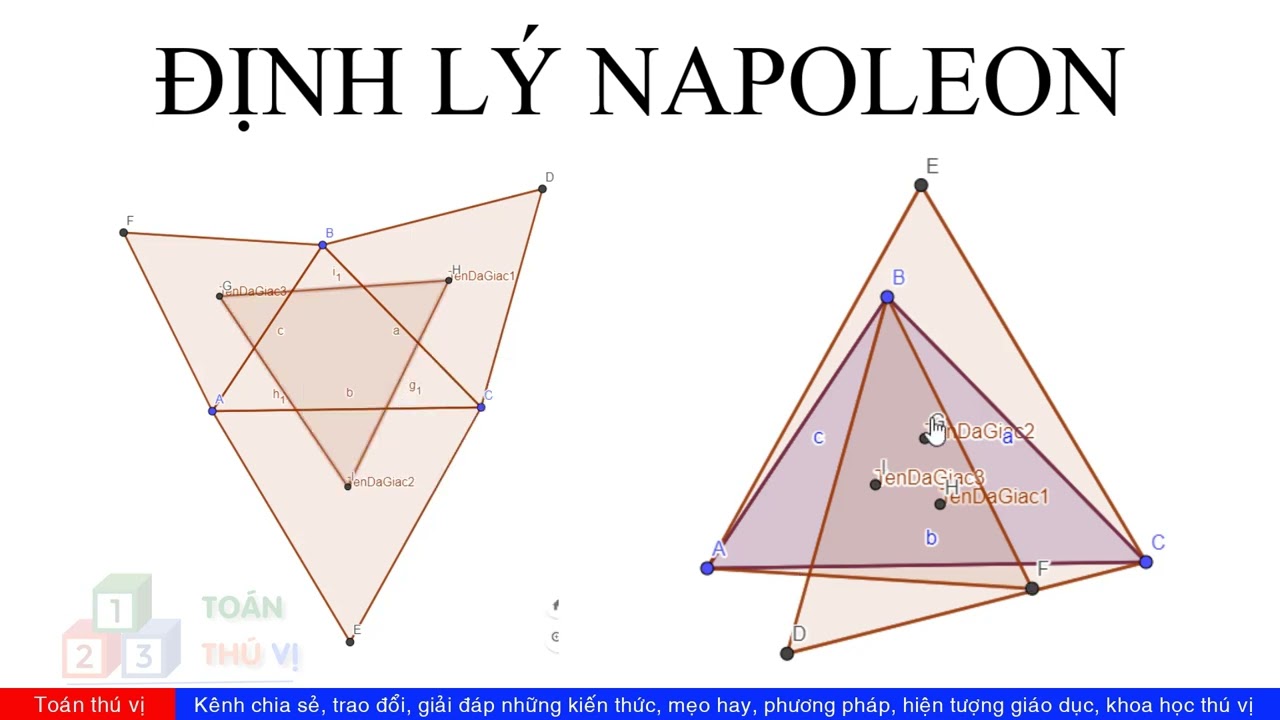
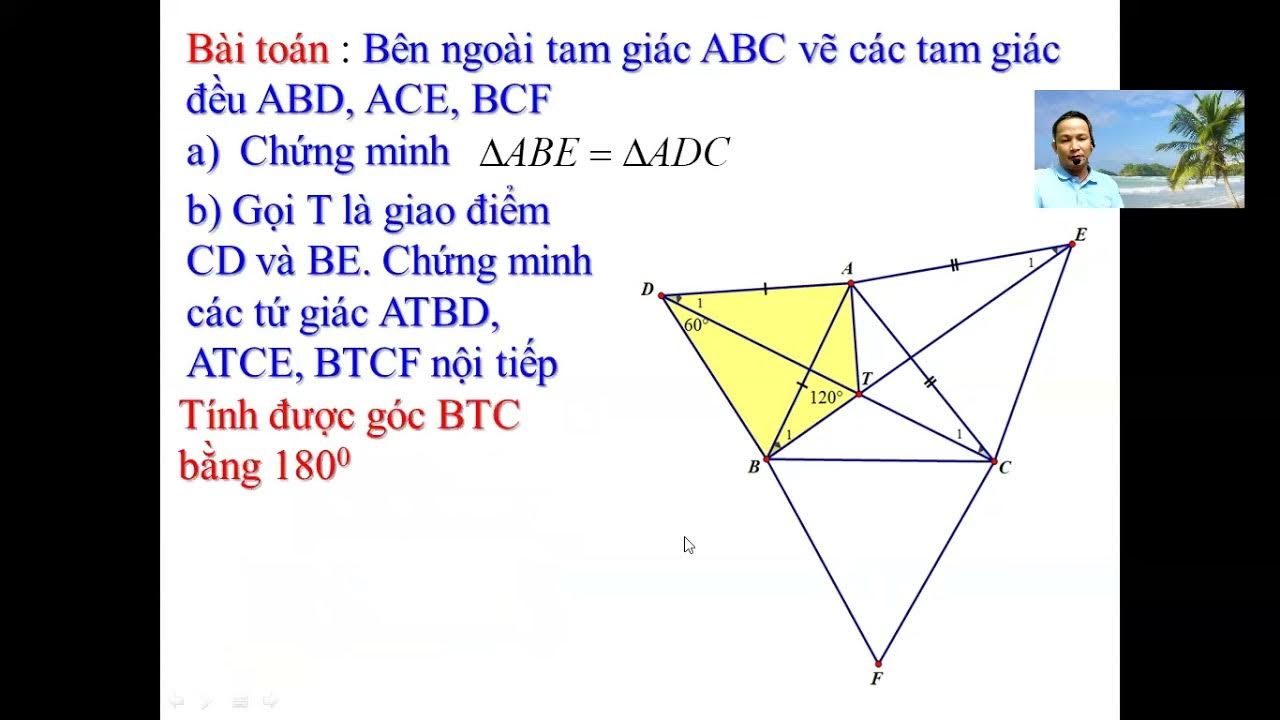
Định lý Napoleon khẳng định rằng nếu ta dựng các tam giác đều trên ba cạnh của một tam giác bất kỳ, thì tâm của ba tam giác đều này tạo thành một tam giác đều. Bài viết này sẽ trình bày chứng minh định lý này bằng phương pháp hình học phẳng.
Chứng minh Định lý Napoleon
Phương pháp sử dụng phép quay
Giả sử tam giác ABC là tam giác bất kỳ. Dựng các tam giác đều BCA', CAB', ABC' hướng ra ngoài tam giác ABC. Gọi G, H, I lần lượt là trọng tâm của các tam giác đều BCA', CAB', ABC'. Ta cần chứng minh tam giác GHI là tam giác đều. Chúng ta sẽ sử dụng phép quay. Quay tam giác đều BCA' quanh điểm B một góc 60 độ theo chiều dương (ngược chiều kim đồng hồ). Điểm A sẽ được ánh xạ vào điểm C, điểm C' sẽ được ánh xạ vào điểm A'. Do đó, tam giác ABC' sẽ được ánh xạ vào tam giác BCA'. Tương tự, ta quay tam giác ABC' quanh C một góc 60 độ theo chiều dương, sẽ được ánh xạ tam giác ABC' vào tam giác ACB'. Kết hợp hai phép quay này, ta thấy rằng phép quay tam giác ABC' quanh B góc 60 độ rồi quanh C góc 60 độ sẽ ánh xạ A vào A'. Phép quay này tương đương với một phép quay quanh một điểm cố định với góc quay 120 độ. Bằng cách sử dụng tính chất của phép quay và mối liên hệ giữa trọng tâm của các tam giác đều, chúng ta có thể chứng minh được tam giác GHI là tam giác đều. Chi tiết tính toán liên quan đến tọa độ phức tạp và cần sử dụng công cụ toán học vector.Phương pháp sử dụng lượng giác
Một phương pháp chứng minh khác sử dụng lượng giác. Chúng ta sẽ biểu diễn tọa độ các đỉnh của tam giác và các trọng tâm của các tam giác đều. Sau đó sử dụng công thức lượng giác để tính khoảng cách giữa các trọng tâm. Việc tính toán này khá phức tạp và cần kiến thức sâu về lượng giác.Tổng kết
Chứng minh Định lý Napoleon có nhiều cách khác nhau, mỗi cách đòi hỏi kiến thức toán học khác nhau. Hai phương pháp trên là hai trong số các phương pháp phổ biến. Việc lựa chọn phương pháp phù hợp phụ thuộc vào trình độ toán học của người đọc. Tuy nhiên, kết quả cuối cùng đều chỉ ra rằng tam giác tạo bởi ba trọng tâm của các tam giác đều dựng trên ba cạnh của một tam giác bất kỳ luôn là tam giác đều.Sản phẩm hữu ích: gió lạnh đầu mùa lớp 8
Sản phẩm liên quan: cach lam chanh muoi
Sản phẩm liên quan: công thức tính cánh vít tải