Chứng minh 3 điểm thẳng hàng lớp 10

Mô tả sản phẩm

Để chứng minh ba điểm thẳng hàng trong lớp 10, ta cần chứng minh chúng cùng nằm trên một đường thẳng. Có nhiều cách để chứng minh điều này, tùy thuộc vào dữ kiện bài toán cho. Bài viết này sẽ trình bày 3 phương pháp thường gặp.

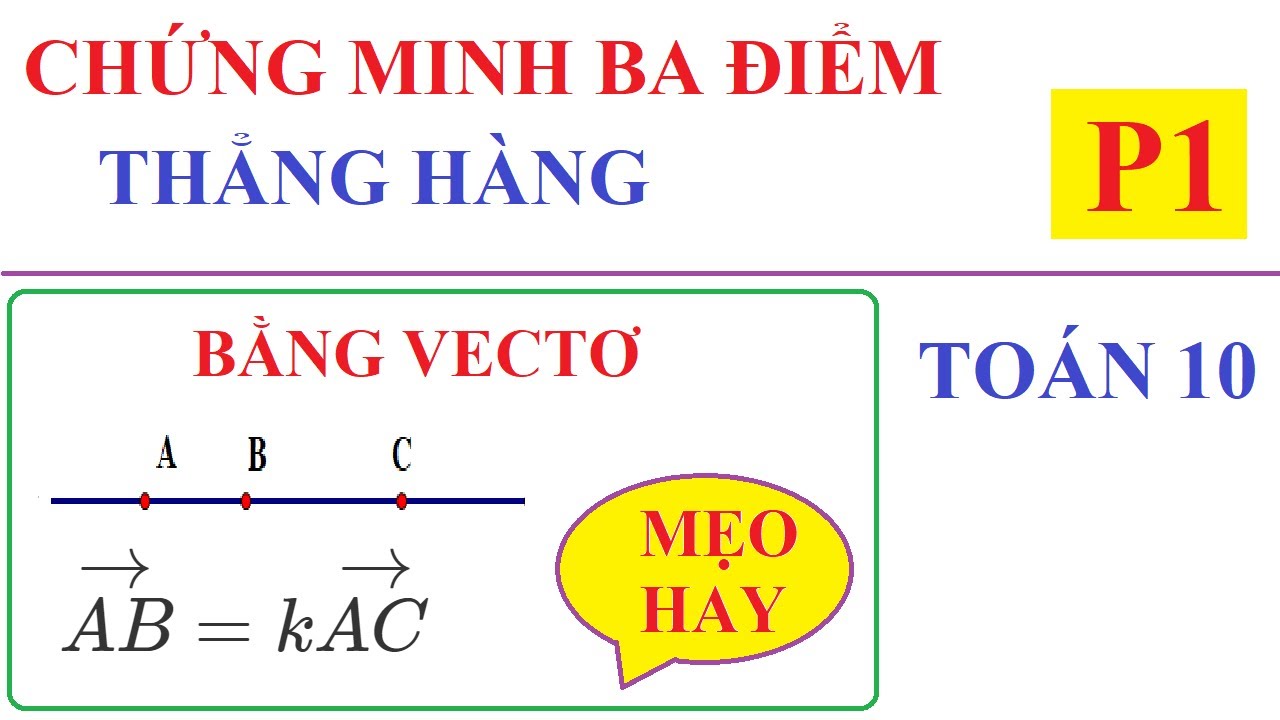
Phương pháp 1: Sử dụng vectơ

Vận dụng tính chất cộng vectơ

Chứng minh ba điểm A, B, C thẳng hàng khi và chỉ khi $\vec{AB}$ và $\vec{AC}$ cùng phương, tức là tồn tại một số k sao cho $\vec{AB}$ = k$\vec{AC}$. Điều này đồng nghĩa với việc tọa độ của hai vectơ tỉ lệ với nhau. Nếu bài toán cho tọa độ của các điểm A, B, C, ta có thể tính tọa độ các vectơ $\vec{AB}$ và $\vec{AC}$, sau đó kiểm tra xem chúng có cùng phương hay không.

Phương pháp 2: Sử dụng hệ số góc

Áp dụng với đường thẳng

Nếu ba điểm A, B, C cùng nằm trên một đường thẳng, thì hệ số góc của đường thẳng AB sẽ bằng hệ số góc của đường thẳng BC (hoặc AC). Phương pháp này thường được áp dụng khi ta đã biết hoặc có thể xác định được phương trình đường thẳng đi qua hai trong ba điểm đó. Ta tính hệ số góc của hai đường thẳng, nếu chúng bằng nhau thì ba điểm thẳng hàng. Lưu ý rằng phương pháp này không áp dụng được cho trường hợp đường thẳng đứng (song song với trục Oy).

Phương pháp 3: Sử dụng định lý Menelaus

Ứng dụng trong tam giác

Định lý Menelaus là một công cụ mạnh mẽ để chứng minh ba điểm thẳng hàng, đặc biệt khi các điểm nằm trên các cạnh của một tam giác. Định lý phát biểu rằng: Cho tam giác ABC và một đường thẳng cắt các cạnh AB, BC, CA lần lượt tại các điểm D, E, F. Khi đó ba điểm D, E, F thẳng hàng khi và chỉ khi: $\frac{AD}{DB} \cdot \frac{BE}{EC} \cdot \frac{CF}{FA} = 1$ Tuy nhiên, phương pháp này cần có sự hiểu biết sâu hơn về định lý Menelaus và thường được sử dụng trong các bài toán hình học phức tạp hơn. Tùy thuộc vào dữ kiện bài toán, bạn nên chọn phương pháp phù hợp nhất để chứng minh ba điểm thẳng hàng. Việc lựa chọn phương pháp hiệu quả sẽ giúp bạn giải quyết bài toán nhanh chóng và chính xác.

Sản phẩm hữu ích: nhóm động vật nào sau đây có hệ tuần hoàn hở

Sản phẩm liên quan: goc giua 2 vecto

Sản phẩm liên quan: các bước tính theo phương trình hóa học

Sản phẩm liên quan: bài hội lim lớp 3