Cạnh của Tam Giác Đều
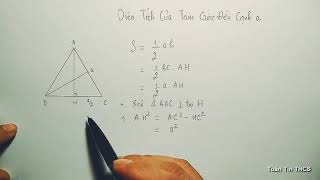
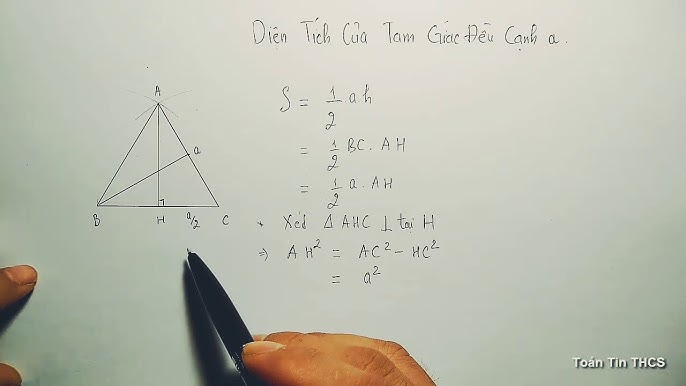

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Cạnh của tam giác đều là độ dài của mỗi cạnh trong hình tam giác đều. Vì là tam giác đều nên cả ba cạnh có độ dài bằng nhau.
Tính cạnh của tam giác đều
Từ diện tích
Nếu biết diện tích (S) của tam giác đều, bạn có thể tính cạnh (a) bằng công thức: a = √(4S / (3√3)).
Từ chu vi
Chu vi (P) của tam giác đều bằng 3 lần độ dài cạnh (a). Do đó, a = P / 3.
Từ chiều cao
Chiều cao (h) của tam giác đều liên hệ với cạnh (a) bởi công thức: h = (a√3) / 2. Từ đó, ta suy ra a = (2h) / √3.
Từ bán kính đường tròn ngoại tiếp
Bán kính đường tròn ngoại tiếp (R) của tam giác đều có liên hệ với cạnh (a) như sau: R = a / √3. Vậy, a = R√3.
Từ bán kính đường tròn nội tiếp
Bán kính đường tròn nội tiếp (r) của tam giác đều liên hệ với cạnh (a) như sau: r = (a√3) / 6. Do đó, a = (6r) / √3 = 2r√3.
Ứng dụng của việc tính cạnh tam giác đều
Việc tính cạnh tam giác đều có nhiều ứng dụng trong toán học, vật lý và kỹ thuật. Ví dụ, trong hình học, nó được sử dụng để tính diện tích, chu vi và các thông số khác của tam giác đều. Trong kỹ thuật, nó được sử dụng trong thiết kế các cấu trúc và máy móc.
Sản phẩm hữu ích: thấu kính hội tụ là thấu kính có
Sản phẩm hữu ích: câu hỏi lớp 2
Sản phẩm liên quan: al + h20 + naoh