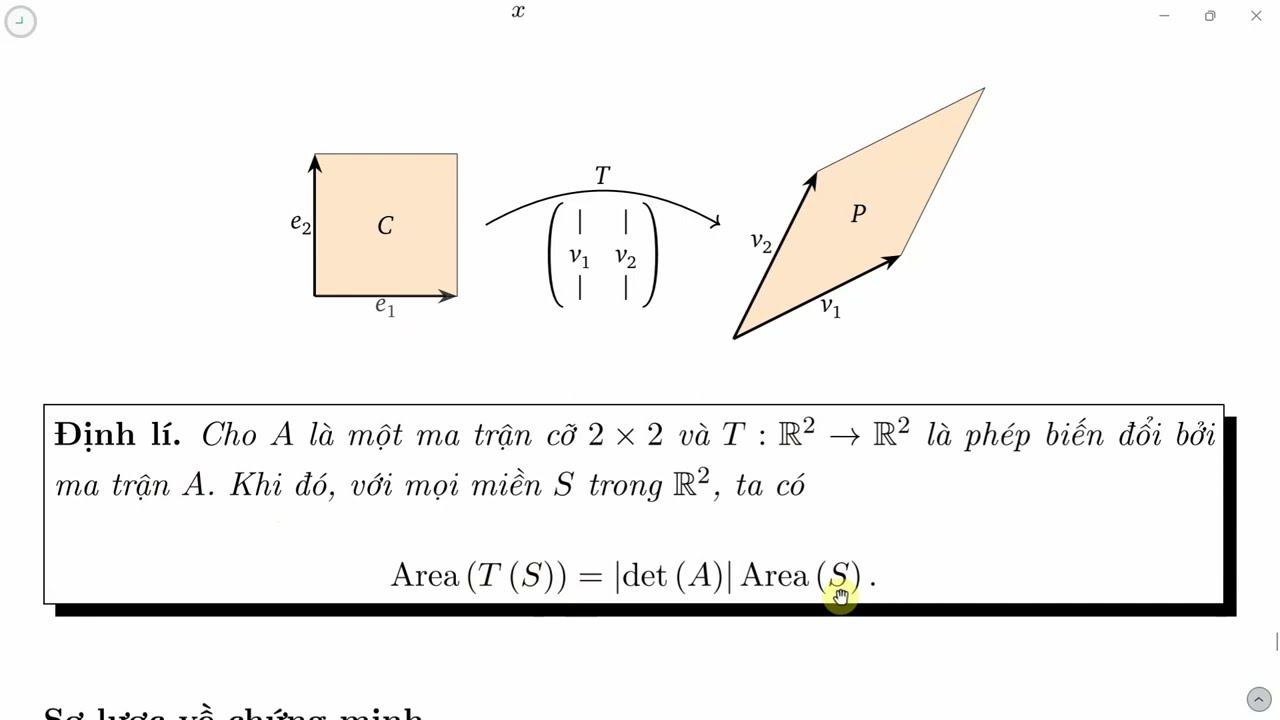
Cách Tính Định Thức

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Cách tính định thức phụ thuộc vào kích thước của ma trận. Với ma trận 1x1, định thức chính là phần tử duy nhất. Đối với ma trận 2x2, 3x3 và các ma trận lớn hơn, ta có những phương pháp khác nhau.
Tính Định Thức Ma Trận 2x2
Công thức tính:
Cho ma trận A = [[a, b], [c, d]], định thức của A (ký hiệu là det(A) hoặc |A|) được tính như sau: det(A) = ad - bc
Ví dụ: Cho ma trận A = [[2, 3], [1, 4]], định thức của A là: det(A) = (2 * 4) - (3 * 1) = 8 - 3 = 5
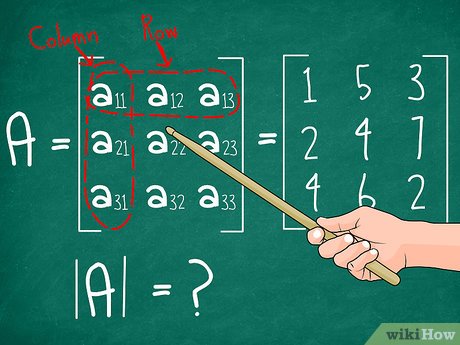
Tính Định Thức Ma Trận 3x3
Quy tắc Sarrus:
Đây là phương pháp dễ nhớ và áp dụng cho ma trận 3x3. Viết lại hai cột đầu tiên của ma trận bên phải cột cuối cùng. Tổng tích các đường chéo chính trừ đi tổng tích các đường chéo phụ sẽ cho ta định thức.
Ví dụ: Cho ma trận A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
det(A) = (1*5*9 + 2*6*7 + 3*4*8) - (3*5*7 + 2*4*9 + 1*6*8) = (45 + 84 + 96) - (105 + 72 + 48) = 225 - 225 = 0
Phát triển theo hàng hoặc cột:
Phương pháp này áp dụng cho ma trận kích thước bất kỳ. Chọn một hàng hoặc cột bất kỳ, nhân mỗi phần tử trong hàng/cột đó với định thức của ma trận con (ma trận thu được bằng cách bỏ đi hàng và cột chứa phần tử đó). Kết quả là tổng đại số các tích này.
Lưu ý: Dấu của mỗi tích sẽ thay đổi luân phiên (+, -, +, -...).
Tính Định Thức Ma Trận NxN (N > 3)
Phát triển theo hàng hoặc cột:
Phương pháp này là cách tổng quát nhất để tính định thức của ma trận kích thước lớn hơn 3. Tuy nhiên, việc tính toán sẽ trở nên phức tạp khi kích thước ma trận tăng lên.
Sử dụng máy tính hoặc phần mềm:
Đối với ma trận kích thước lớn, việc sử dụng máy tính hoặc phần mềm toán học như Matlab, Mathematica, ... là cần thiết để tính toán định thức một cách hiệu quả.
Hiểu được cách tính định thức là rất quan trọng trong nhiều lĩnh vực toán học và khoa học ứng dụng, đặc biệt là giải hệ phương trình tuyến tính, tìm ma trận nghịch đảo, và xác định tính khả nghịch của ma trận.
Sản phẩm hữu ích: lá é là gì
Sản phẩm liên quan: trong công thức cs2 tổng số cặp electron lớp ngoài cùng của c và s chưa tham gia liên kết là
Xem thêm: mua giống cây la hán quả ở đâu