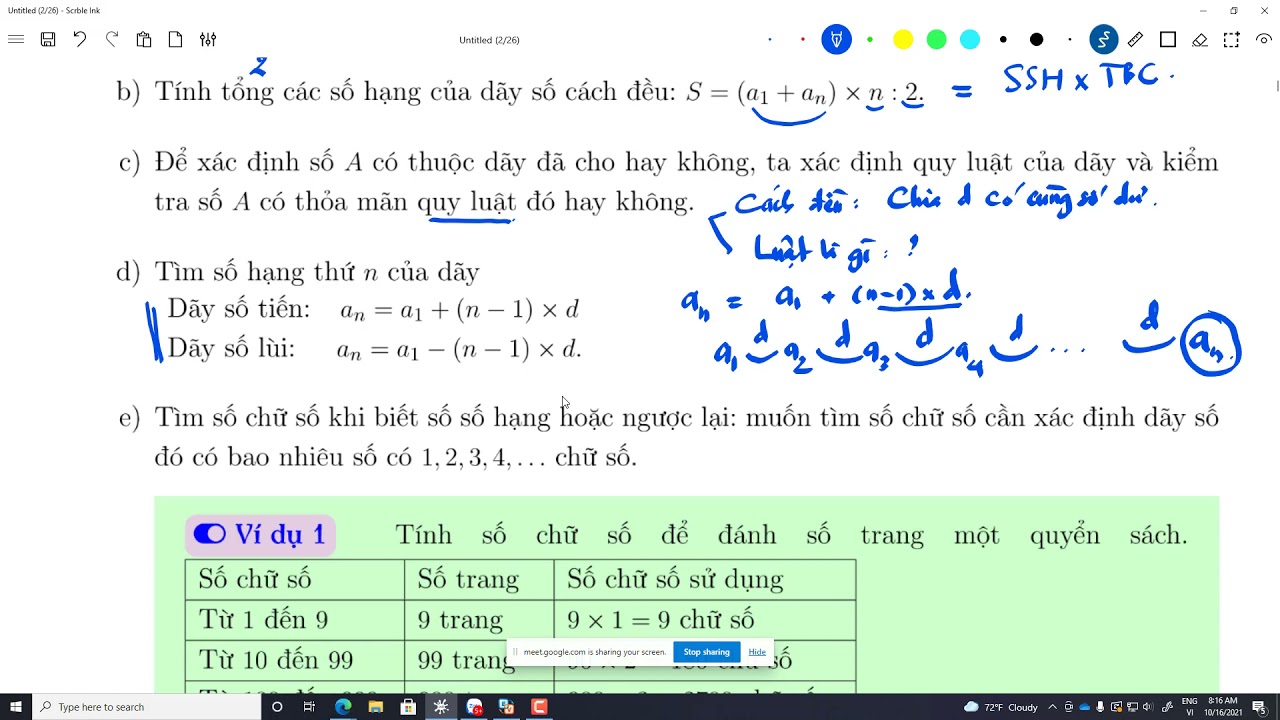
Cách Tìm Quy Luật Của Dãy Số Lớp 4

Mô tả sản phẩm

Tìm quy luật của dãy số là một kỹ năng quan trọng giúp các em học sinh lớp 4 phát triển tư duy logic và khả năng giải quyết vấn đề. Bài viết này sẽ hướng dẫn các em cách tìm quy luật của dãy số một cách dễ hiểu và hiệu quả.

Các bước tìm quy luật của dãy số

1. Quan sát và nhận biết sự khác biệt giữa các số

Đầu tiên, hãy quan sát kỹ dãy số và tìm xem có sự khác biệt nào giữa các số liên tiếp hay không. Sự khác biệt này có thể là phép cộng, phép trừ, phép nhân, phép chia hoặc sự kết hợp của các phép tính này. Ví dụ, trong dãy số 2, 4, 6, 8, ..., sự khác biệt giữa các số liên tiếp là 2 (4-2=2, 6-4=2, 8-6=2...).

2. Xác định quy luật

Sau khi tìm ra sự khác biệt, hãy xem xét xem sự khác biệt đó có lặp lại đều đặn hay không. Nếu có, đó chính là quy luật của dãy số. Ví dụ, trong dãy số 1, 4, 7, 10, ..., sự khác biệt giữa các số liên tiếp là 3 (4-1=3, 7-4=3, 10-7=3...), vậy quy luật của dãy số này là cộng 3.

3. Kiểm tra quy luật

Sau khi tìm ra quy luật, hãy kiểm tra xem quy luật đó có đúng với tất cả các số trong dãy hay không. Nếu đúng, bạn đã tìm ra quy luật của dãy số. Nếu không, hãy xem xét lại các bước trên và tìm kiếm quy luật khác.

4. Một số dạng quy luật phổ biến

* **Cộng hoặc trừ một số cố định:** Đây là dạng quy luật đơn giản nhất. Ví dụ: 2, 5, 8, 11,... (cộng 3) * **Nhân hoặc chia một số cố định:** Ví dụ: 3, 6, 12, 24,... (nhân 2) * **Quy luật tăng dần hoặc giảm dần:** Ví dụ: 10, 8, 6, 4,... (giảm 2) * **Quy luật lặp lại:** Ví dụ: 1, 2, 3, 1, 2, 3,... (lặp lại chu kỳ 1,2,3) * **Quy luật kết hợp:** Một số dãy số phức tạp hơn có thể kết hợp nhiều quy luật khác nhau.

5. Bài tập ví dụ

Hãy tìm quy luật của dãy số sau: 1, 3, 6, 10, 15,... Gợi ý: Quan sát sự khác biệt giữa các số liên tiếp: 3-1=2, 6-3=3, 10-6=4, 15-10=5. Sự khác biệt tăng dần 1 đơn vị mỗi lần. Đây là một dãy số có quy luật cộng dồn.

Sản phẩm hữu ích: phương trình al + hno3

Sản phẩm hữu ích: cl2 cl- + clo3-

Xem thêm: trạng ngữ là gì cho ví dụ

Sản phẩm liên quan: bài thơ từ ấy lớp 11