Các Trường Hợp Tam Giác Vuông Bằng Nhau

Mô tả sản phẩm

Có bốn trường hợp bằng nhau của hai tam giác vuông. Hiểu rõ các trường hợp này giúp bạn giải quyết nhiều bài toán hình học một cách dễ dàng và chính xác.

Tổng Quan Về Các Trường Hợp Tam Giác Vuông Bằng Nhau

Điều Kiện Cần Và Đủ Để Hai Tam Giác Vuông Bằng Nhau

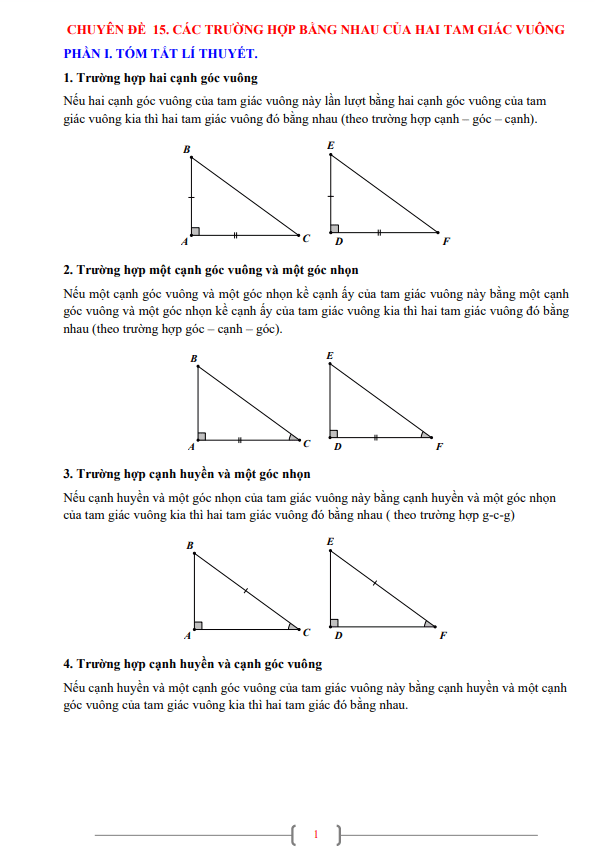
Hai tam giác vuông bằng nhau khi chúng thỏa mãn một trong bốn trường hợp sau:
1. Trường hợp cạnh huyền - cạnh góc vuông (ch-cgv): Hai tam giác vuông bằng nhau nếu cạnh huyền và một cạnh góc vuông của tam giác này bằng cạnh huyền và một cạnh góc vuông của tam giác kia.
2. Trường hợp hai cạnh góc vuông (cgv-cgv): Hai tam giác vuông bằng nhau nếu hai cạnh góc vuông của tam giác này bằng hai cạnh góc vuông của tam giác kia.
3. Trường hợp cạnh huyền - góc nhọn (ch-gn): Hai tam giác vuông bằng nhau nếu cạnh huyền và một góc nhọn của tam giác này bằng cạnh huyền và một góc nhọn của tam giác kia.
4. Trường hợp góc nhọn - cạnh góc vuông (gn-cgv): Hai tam giác vuông bằng nhau nếu một góc nhọn và một cạnh góc vuông của tam giác này bằng một góc nhọn và một cạnh góc vuông của tam giác kia.

Ứng Dụng Của Các Trường Hợp Tam Giác Vuông Bằng Nhau

Việc hiểu rõ các trường hợp bằng nhau của tam giác vuông là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn, đặc biệt trong chương trình hình học lớp 8 và các lớp trên. Từ việc chứng minh các đoạn thẳng bằng nhau, tính độ dài các cạnh chưa biết đến việc xác định mối quan hệ giữa các góc và cạnh trong hình học không gian, việc nắm vững kiến thức này đều rất cần thiết.

Lưu ý quan trọng

Khi áp dụng các trường hợp bằng nhau của tam giác vuông, cần phải xác định chính xác các yếu tố tương ứng (cạnh huyền, cạnh góc vuông, góc nhọn) của hai tam giác để tránh sai sót.

Sản phẩm hữu ích: bảng tính tan đầy đủ

Xem thêm: trung du và miền núi bắc bộ không có thế mạnh nổi bật nào sau đây?

Sản phẩm hữu ích: công thức tính khoảng cách lớp 12

Xem thêm: oxit nào là oxit lưỡng tính

Sản phẩm liên quan: giới hạn đo là gì