Công thức tính khoảng cách lớp 12


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Công thức tính khoảng cách trong chương trình Toán lớp 12 phụ thuộc vào đối tượng cần tính khoảng cách. Có nhiều công thức khác nhau, tùy thuộc vào việc bạn cần tính khoảng cách giữa điểm và mặt phẳng, điểm và đường thẳng, hay giữa hai đường thẳng chéo nhau.
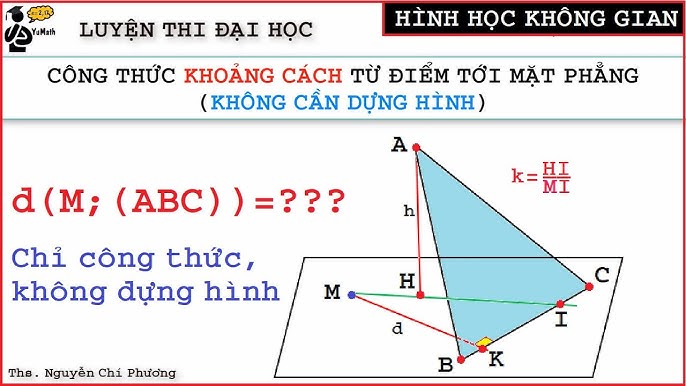
Khoảng cách từ điểm đến mặt phẳng
Công thức tổng quát:
Khoảng cách từ điểm M(x0; y0; z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 được tính theo công thức:
d(M, (P)) = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2)
Khoảng cách từ điểm đến đường thẳng
Trong không gian:
Để tính khoảng cách từ điểm M đến đường thẳng Δ, ta cần tìm hình chiếu vuông góc H của M trên Δ. Khoảng cách cần tìm là MH. Công thức tính toán khá phức tạp và thường được giải quyết bằng phương pháp vectơ. Việc thiết lập phương trình đường thẳng Δ và áp dụng công thức độ dài vectơ là cần thiết. Thường sẽ được giải quyết bằng các phương pháp tọa độ không gian.
Trên mặt phẳng:
Công thức tính khoảng cách từ điểm M(x0; y0) đến đường thẳng ax + by + c = 0 là:
d(M, Δ) = |ax0 + by0 + c| / √(a2 + b2)
Khoảng cách giữa hai đường thẳng chéo nhau
Công thức tổng quát:
Khoảng cách giữa hai đường thẳng chéo nhau Δ1 và Δ2 là độ dài đoạn thẳng ngắn nhất nối hai đường thẳng đó. Tính toán thường phức tạp và liên quan đến việc tìm vectơ chỉ phương của hai đường thẳng và một vectơ pháp tuyến chung. Kết quả thường được tính thông qua tích có hướng và độ dài vectơ.
Sản phẩm liên quan: tính chất khối chóp đều
Sản phẩm hữu ích: đề kiểm tra toán lớp 3 cuối kì 2
Sản phẩm liên quan: bd plus nhan dinh