Góc Lượng Giác Đặc Biệt
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Các góc lượng giác đặc biệt là những góc có giá trị sin, cos, tan và cot dễ dàng tính toán và thường được sử dụng trong toán học và vật lý. Bài viết này sẽ giúp bạn hiểu rõ hơn về các góc lượng giác đặc biệt và cách tính các giá trị lượng giác của chúng.
Các Góc Lượng Giác Đặc Biệt Thường Gặp
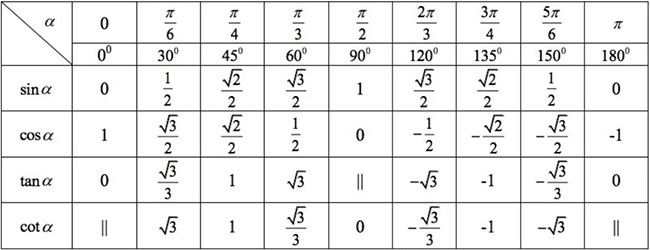
Góc 0, π/6, π/4, π/3, π/2, π, 3π/2, 2π (và các góc cùng cung)
Đây là những góc lượng giác đặc biệt cơ bản nhất. Bạn cần nắm vững giá trị sin, cos, tan và cot của các góc này. Chúng ta có thể sử dụng vòng tròn lượng giác để dễ dàng hình dung và nhớ các giá trị này. Ví dụ: sin(π/6) = 1/2, cos(π/4) = √2/2, tan(π/3) = √3, v.v... Việc ghi nhớ các giá trị này sẽ giúp bạn giải quyết nhanh chóng các bài toán liên quan.
Cách Tính Giá Trị Lượng Giác của Góc Đặc Biệt
Sử dụng Vòng Tròn Lượng Giác
Vòng tròn lượng giác là công cụ trực quan hữu hiệu để xác định giá trị lượng giác của các góc. Bằng cách xác định vị trí của góc trên vòng tròn, ta dễ dàng tìm được giá trị sin, cos, tan và cot tương ứng. Hãy luyện tập vẽ và sử dụng vòng tròn lượng giác để làm quen với các góc đặc biệt.
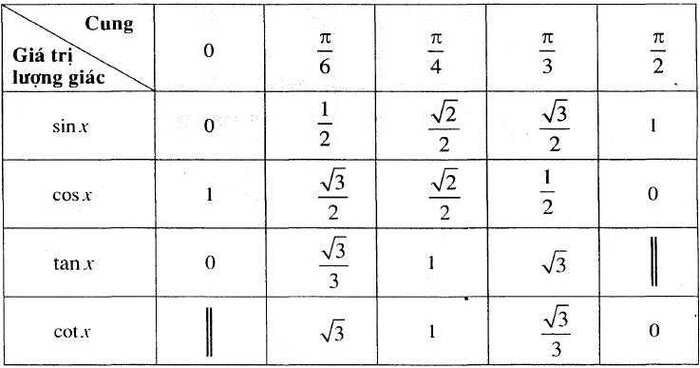
Sử dụng Bảng Giá Trị Lượng Giác
Một cách khác để tìm giá trị lượng giác của các góc đặc biệt là sử dụng bảng giá trị lượng giác. Tuy nhiên, việc ghi nhớ bảng này có thể khó khăn, do đó, việc hiểu và sử dụng vòng tròn lượng giác vẫn là phương pháp hiệu quả hơn.
Ứng Dụng của Góc Lượng Giác Đặc Biệt
Góc lượng giác đặc biệt được ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt là trong giải tích, hình học và vật lý. Ví dụ, trong việc tính toán quãng đường, vận tốc, gia tốc trong chuyển động tròn đều, việc nắm vững các giá trị lượng giác của góc đặc biệt là rất cần thiết.
Hiểu rõ về các góc lượng giác đặc biệt sẽ giúp bạn giải quyết nhanh chóng và chính xác các bài toán liên quan đến lượng giác, từ đó nâng cao khả năng toán học của bạn. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!
Sản phẩm liên quan: cách đổi đơn vị mét khối
Sản phẩm hữu ích: ch3cooh + c2h5oh xúc tác h2so4
Xem thêm: phương pháp dạy toán lớp 2
Sản phẩm hữu ích: rơi tự do là chuyển động
Xem thêm: 1π bằng bao nhiêu tiền việt